Proba, variable aléatoire et code..

[thojo]

Bonjour, je ne comprends pas un élément de cet exo :

La fermeture de sécurité d’un portable est assurée par la composition d’un code de 3 chiffres, obtenu en faisant tourner 3 molettes portant les chiffres de 0 à 9.
Une personne compose au hasard un code.
On donne les evts : A : « le code est bon »
B : « le code est formé de 3 chiffres distincts »
C : « le code comporte 2 chiffres identiques et 2 seulement »
On demande de déterminer p(A), p(B), et p(C).

Il y a 10*10*10 cas possibles (de combinaisons)

Il y a 1*1*1 code permettant d’ouvrir le cartable, donc p(A) = 1/1000

Il y a 10 possibilités de choisir le 1er chiffre du code. Une fois celui-ci choisi il y a 9 possibilités pour choisir le 2ème chiffre (ils doivent être distincts) et ensuite 8 possibilités de choix du dernier car celui-ci doit être distinct des 2 premiers. Donc : il y 10*9*8 cas possibles d’avoir un code formé de 3 chiffres distincts. Et p(B) = 10*9*8/1000

Pour a dernière question le corrigé dit ceci :
On remarque qu’un code est constitué :
- de 3 chiffres distincts ou de
- 2 chiffres identiques (et que 2)
- Ou de 3 chiffres identiques (appelons D cet évt et p(D) = 10/1000)
Donc p(C) = 1 – p(B) – p(D) = 1-0,72 = 0,27
Je comprends tout cela, mais mon premier reflex pour trouver p(C) a été de raisonner comme pour les autres proba : au départ on a 10 possibilités de choisir le 1er chiffre, ensuite 1 possibilité de choisit le même chiffre que le premier, puis, comme le troisième doit être différent, 9 possibilités de choisir le 3ème chiffre. Donc au total : 10*1*9 cas possibles d’avoir 2 chiffres identiques et 2 seulement.. et p(C) = 90/1000 ce qui ne correspond pas au résultat du corrigé.. ou alors faut-il multiplier ce résultat par 3, étant donné qu’il y a 3 possibilités pour que 2 chiffres seulement soient égaux : un en premier, l’autre en 2ème, l’un en 2ème, l’autre en 3ème, puis l’un en 1er et l’autre en 3ème ? ce qui donnerait 90*3 et p(C)= 90* 3/1000 = 0,27 ?? je viens de me rendre compte que c’est le même résultat donc ça doit être cela non ?

[Jota Be]

Bonjour, je ne comprends pas un élément de cet exo :

La fermeture de sécurité d’un portable est assurée par la composition d’un code de 3 chiffres, obtenu en faisant tourner 3 molettes portant les chiffres de 0 à 9.
Une personne compose au hasard un code.
On donne les evts : A : « le code est bon »
B : « le code est formé de 3 chiffres distincts »
C : « le code comporte 2 chiffres identiques et 2 seulement »
On demande de déterminer p(A), p(B), et p(C).

Il y a 10*10*10 cas possibles (de combinaisons)

Il y a 1*1*1 code permettant d’ouvrir le cartable, donc p(A) = 1/1000

Il y a 10 possibilités de choisir le 1er chiffre du code. Une fois celui-ci choisi il y a 9 possibilités pour choisir le 2ème chiffre (ils doivent être distincts) et ensuite 8 possibilités de choix du dernier car celui-ci doit être distinct des 2 premiers. Donc : il y 10*9*8 cas possibles d’avoir un code formé de 3 chiffres distincts. Et p(B) = 10*9*8/1000

Pour a dernière question le corrigé dit ceci :
On remarque qu’un code est constitué :
- de 3 chiffres distincts ou de
- 2 chiffres identiques (et que 2)
- Ou de 3 chiffres identiques (appelons D cet évt et p(D) = 10/1000)
Donc p(C) = 1 – p(B) – p(D) = 1-0,72 = 0,27
Je comprends tout cela, mais mon premier reflex pour trouver p(C) a été de raisonner comme pour les autres proba : au départ on a 10 possibilités de choisir le 1er chiffre, ensuite 1 possibilité de choisit le même chiffre que le premier, puis, comme le troisième doit être différent, 9 possibilités de choisir le 3ème chiffre. Donc au total : 10*1*9 cas possibles d’avoir 2 chiffres identiques et 2 seulement.. et p(C) = 90/1000 ce qui ne correspond pas au résultat du corrigé.. ou alors faut-il multiplier ce résultat par 3, étant donné qu’il y a 3 possibilités pour que 2 chiffres seulement soient égaux : un en premier, l’autre en 2ème, l’un en 2ème, l’autre en 3ème, puis l’un en 1er et l’autre en 3ème ? ce qui donnerait 90*3 et p(C)= 90* 3/1000 = 0,27 ?? je viens de me rendre compte que c’est le même résultat donc ça doit être cela non ?

Salut,
tout à fait, ton raisonnement est bon puisque comme tu l'as dit, tu ne peux placer les chiffres identiques que de trois manières différentes et seulement trois (sorte de "permutation circulaire", mais je préfère ne pas trop employer ce mot puisque c'est en dehors de mon champ de connaissances !).

[geegee]

Bonjour, je ne comprends pas un élément de cet exo :

La fermeture de sécurité d’un portable est assurée par la composition d’un code de 3 chiffres, obtenu en faisant tourner 3 molettes portant les chiffres de 0 à 9.
Une personne compose au hasard un code.
On donne les evts : A : « le code est bon »
B : « le code est formé de 3 chiffres distincts »
C : « le code comporte 2 chiffres identiques et 2 seulement »
On demande de déterminer p(A), p(B), et p(C).

Il y a 10*10*10 cas possibles (de combinaisons)

Il y a 1*1*1 code permettant d’ouvrir le cartable, donc p(A) = 1/1000

Il y a 10 possibilités de choisir le 1er chiffre du code. Une fois celui-ci choisi il y a 9 possibilités pour choisir le 2ème chiffre (ils doivent être distincts) et ensuite 8 possibilités de choix du dernier car celui-ci doit être distinct des 2 premiers. Donc : il y 10*9*8 cas possibles d’avoir un code formé de 3 chiffres distincts. Et p(B) = 10*9*8/1000

Pour a dernière question le corrigé dit ceci :
On remarque qu’un code est constitué :
- de 3 chiffres distincts ou de
- 2 chiffres identiques (et que 2)
- Ou de 3 chiffres identiques (appelons D cet évt et p(D) = 10/1000)
Donc p(C) = 1 – p(B) – p(D) = 1-0,72 = 0,27
Je comprends tout cela, mais mon premier reflex pour trouver p(C) a été de raisonner comme pour les autres proba : au départ on a 10 possibilités de choisir le 1er chiffre, ensuite 1 possibilité de choisit le même chiffre que le premier, puis, comme le troisième doit être différent, 9 possibilités de choisir le 3ème chiffre. Donc au total : 10*1*9 cas possibles d’avoir 2 chiffres identiques et 2 seulement.. et p(C) = 90/1000 ce qui ne correspond pas au résultat du corrigé.. ou alors faut-il multiplier ce résultat par 3, étant donné qu’il y a 3 possibilités pour que 2 chiffres seulement soient égaux : un en premier, l’autre en 2ème, l’un en 2ème, l’autre en 3ème, puis l’un en 1er et l’autre en 3ème ? ce qui donnerait 90*3 et p(C)= 90* 3/1000 = 0,27 ?? je viens de me rendre compte que c’est le même résultat donc ça doit être cela non ?

La fermeture de sécurité d’un portable est assurée par la composition d’un code de 3 chiffres, obtenu en faisant tourner 3 molettes portant les chiffres de 0 à 9.
Une personne compose au hasard un code.
On donne les evts : A : « le code est bon »
B : « le code est formé de 3 chiffres distincts »
C : « le code comporte 2 chiffres identiques et 2 seulement »
p(A)=1/10*10*10=1/1000
p(B)= 10*9*8/1000 = 720/1000
p(C)=3*10*10/1000 = 300/1000

[thojo]

merci pour vos réponses, mais Geegee il me semble que ce n'est pas cela pour p(C) comme il a été dit plus haut..

[Dlzlogic]

@geegee,
Il me semble que thojo ne demandait pas la réponse, puisqu'il avait la correction, mais une explication.
On a du mal à faire expliquer par les élèves ce qu'est leur énoncé, alors, lorsqu'il demandent une explication, la réponse, sans aucun commentaire, ils s'en fichent.

[geegee]

Bonjour,

il y a 10*10*10 cas de numeros possible sous forme d'arbre.

Si trois nombre distint 10*(10-1)*(10-2)

[Iroh]

Pour la C): si on note un chiffre, et un autre chiffre. On cherche la probabilité d'avoir:
(;),;),;)) ou (;),;),;)) ou (;),;),;))

Pour (;),;),;)), un choisi d'abord un chiffre, n'importe lequel, la probabilité de piocher n'importe quel chiffre vaut 1, puis on veux piocher le même, on a 1 chance sur 10, puis un chiffre différent, 9 chance sur 10. La proba d'avoir (;),;),;)) vaut

Il faut aussi ajouter la proba d'avoir (;),;),;)), ou (;),;),;)). On constate que cette proba est la même que celle calculée, donc au final on a: P[C] = 3*0.09 = 0.27.

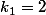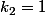Le "3" correspond en fait au nombre de permutations de 3 élements avec (les ) et (les ) non distincts. Ça vaut: