Morgaanee a écrit:Bonjour à tous, j'ai un devoir à faire pour demain mais je ne comprend absolument pas ce qu'il faut faire pour cet exercice ..
Voici l'énoncé : La figure ci-contre représente un cercle de rayon R, un carré inscrit dans ce cercle, un cercle inscrit dans ce carré et ainsi de suite
1- On a tracé quatre cercles et quatre carrés. Déterminer l'aire totale des zones colorées en fonction de R.
2- Vers quelle limite tend l'aire totale des zones colorées lorsque l'on poursuit la construction indéfiniment ?
Intuitivement je dirais 0 mais cela reste à prouver ...
Merci d'avance à tous 
Si j'ai bien compris, il t'est demandé de calculer les deux aires colorées.
Tu peux noter une chose : c'est que dès que tu en connaîtras une, tu connaîtras l'autre puisque la somme des deux forme un disque :+++:
1. Si j'appelle

le plus grand des cercles (celui de rayon

),

le carré inscrit dedans et
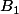
la première aire bleue telle que
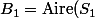-{\rm Aire}(C_1))
.
Que vaut
)
? Que vaut
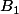
?
Soient maintenant

le cercle inscrit dans
)
(donc de rayon strictement plus petit que R),

le carré inscrit dedans et
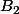
la seconde aire bleue telle que
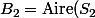-{\rm Aire}(C_2))
.
Que vaut
)
? Que vaut
)
? Déduis-en
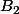
:++:
...
2. Une première remarque : On effectue des sommes d'aires de plus en plus petites, mais une aire étant positive (en particulier les premières le sont strictement), la somme des aires ne pourra jamais tendre vers 0 lorsqu'on répète le processus à l'infini.

