Priorité d'une opération
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 27 Aoû 2009, 16:38
par cookiie » 27 Aoû 2009, 16:38
Ericovitchi a écrit: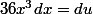
est-ce que tu as compris comment on obtiens ça déjà ? (il suffit de prendre la différentielle des deux cotés)
donc je remplace
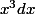
par
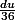
et le
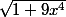
par
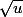
Tu n'as jamais encore calculé d'intégrale ou fait de changement de variable ? c'est une intégrale très simple.
Après il faut trouver la primitive de
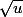
tu as trouvé quoi ? rétablir les x et calculer entre les bornes.
J'en ai fait des tonnes d'integrales mais celle ci ne passe pas dutout :triste:
Je ne sais pas ce que c'est la différentielle mais moi je trouve ca en faisant simplement la dérivée.
et le 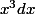 par
par 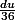
Ca je ne comprend pas pourquoi un tel remplacement, je ne vois pas d'ou ca viens enfait.TEX]x^3dx [/TEX] par
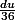
tout simplement car comme ca x^3 est égal à Du !
Ah et la primitive de
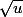
serait


-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Aoû 2009, 17:46
par Ericovitchi » 27 Aoû 2009, 17:46
alors ne parlons pas de différentielle. Posons juste
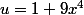
calcule

remplaces dans ton équation

par u'/36
ca te donne

et u' = du/dx donc on retombe sur
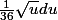
Ah et la primitive de
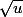
serait

non tu oublies le coefficient. la primitive de
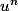
c'est

il est passé où le n+1 ?
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 27 Aoû 2009, 17:54
par cookiie » 27 Aoû 2009, 17:54
Ericovitchi a écrit:alors ne parlons pas de différentielle. Posons juste
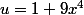
calcule

remplaces dans ton équation

par u'/36
ca te donne

et u' = du/dx donc on retombe sur
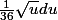
non tu oublies le coefficient. la primitive de
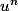
c'est

il est passé où le n+1 ?
Merci

ah :mur: je suis grave .. c'est simplement ca .. Lol !
Tu a raison j'ai oublié le n+1 !
Tanto je cafouillais grave , de plus il y a deux changements de bornes à faire aussi après ca , hopla au boulot :zen:
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 27 Aoû 2009, 18:21
par cookiie » 27 Aoû 2009, 18:21
c'est pas possible.. quand l'integrale ne pose plus de problème c'est au tour du changement de bornes !
En remplacant à partir de T :
x= -1 ----> -8
x= 0 ----> 0
et
x= 0 ----> 1
x= 2 -----> 145
je ne vous dis même pas ce que ca donne numériquement !
 ^3/2)
c'est mon integrale..
j'pense que je vais laisser tomber :doh:

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Aoû 2009, 19:25
par Ericovitchi » 27 Aoû 2009, 19:25
c'est quoi encore tout ça. Ils sortent d'où les 2 pi ?
On en était à
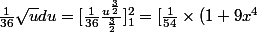^{\frac {3}{2}}] _{1}^2= ...)
-
echevaux
- Membre Relatif
- Messages: 276
- Enregistré le: 06 Juin 2006, 16:08
-
 par echevaux » 27 Aoû 2009, 20:28
par echevaux » 27 Aoû 2009, 20:28
Ericovitchi a écrit:... il faut trouver
la primitive de

...
cookiie a écrit:Ah et
la primitive de

serait
Ericovitchi a écrit:...
la primitive de

c'est ...
Je croyais que cette fonction (tout comme beaucoup d'autres) avait une infinité de primitives ...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Aoû 2009, 21:41
par Ericovitchi » 27 Aoû 2009, 21:41
oui oui oui OK une infinité à une constante prêt. Pinaillou :look2:
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 28 Aoû 2009, 10:27
par cookiie » 28 Aoû 2009, 10:27
Ericovitchi a écrit:c'est quoi encore tout ça. Ils sortent d'où les 2 pi ?
On en était à
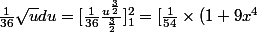^{\frac {3}{2}}] _{1}^2= ...)
les 2 Pi sortent de la formule qui sert à trouver les unitées d'aire de la surface d'un solide de révolution..

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 28 Aoû 2009, 10:53
par Ericovitchi » 28 Aoû 2009, 10:53
:stupid: Qu'est ce que viennent foutre des solides de révolution là-dedans, tu es vraiment en plein délire. Tu es en train de calculer une bête intégrale, tu en es à
^{\frac {3}{2}}] _{1}^2)
. le résultat est
31,7483.
salut et bonne chance mais tu devrais vraiment réviser les intégrales et essayer de pas tout mélanger. :--:
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 28 Aoû 2009, 11:20
par cookiie » 28 Aoû 2009, 11:20
Ericovitchi a écrit::stupid: Qu'est ce que viennent foutre des solides de révolution là-dedans, tu es vraiment en plein délire. Tu es en train de calculer une bête intégrale, tu en es à
^{\frac {3}{2}}] _{1}^2)
. le résultat est
31,7483.
salut et bonne chance mais tu devrais vraiment réviser les intégrales et essayer de pas tout mélanger. :--:
Merci mais je ne mélange rien. Je cite :
Calculer l'aire de la surface de révolution et le volume du solide de révolution engendré par la rotation autour de l'ace des X fr la fonction x^3 entre -1 et 2
Je fais mon graphique je vois qu'il y a une partie négative entre -1 et 0 et une partie positive entre 1 et 2 Donc je décide de calculer d'abord la partie négative et ensuite la partie positive.
pour ce faire j'ai une formule.
 \sqrt{ 1 +f'(x)^2})
Et voila d'ou sort le 2 pi. Je n'en ai pas tenu compte car étant une constante je m'en préoccupe seulement lors du calcul des bornes dans l'integrale que j'ai simplifié :happy2:
Tu comprends mieux ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 28 Aoû 2009, 11:23
par Ericovitchi » 28 Aoû 2009, 11:23
ha oui OK je comprend mieux en relisant ton premier post. effectivement.
excuses moi pour mes remarques alors.
-
cookiie
- Membre Naturel
- Messages: 35
- Enregistré le: 22 Aoû 2009, 07:11
-
 par cookiie » 28 Aoû 2009, 11:27
par cookiie » 28 Aoû 2009, 11:27
Ericovitchi a écrit:ha oui OK je comprend mieux en relisant ton premier post. effectivement.
excuses moi pour mes remarques alors.
Pas de soucis :we: et merci pour ton aide

Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
est-ce que tu as compris comment on obtiens ça déjà ? (il suffit de prendre la différentielle des deux cotés)
par
par
tu as trouvé quoi ? rétablir les x et calculer entre les bornes.

 ...
... c'est ...
c'est ...