Primitive

[zher007]

Salut à tous j'ai un problème avec cette primitive: [ (dx/cos(x))

j'ai la réponse mais je ne sais pas comment y arriver: ln l(1+sin(x))/cosx)l + k

merci à l'avance

[lapras]

Que recherches tu ? La primitive de 1/cos(x) ?
Si oui, j'ai une idée avec changement de variable

[fonfon]

salut,

je sais pas si c'est niveau lycée

sinon



ensuite tu poses sin(x)=t donc cos(x)dx=dt

donc



or

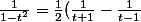et là plus de difficulté

[lapras]

Fonfon
je proposerais autre chose :

Calculer :
Int ( (1+t²) * 1/(1-t²) dx)
avec t = tan(x/2)

En faisant une IPP on peut y arriver il me semble !
On peut le faire avec dt en dérivant 1+t²
sachant que tan(x)' = -ln(cos(x))

[Nightmare]

Bonjour,

d'une part, parler de "LA" primitive est incorrect, d'autre part, la réponse : ln l(1+sin(x))/cosx)l + k est fausse car le domaine de primitivation n'est pas connexe.

[lapras]

EDIT :
j'ai compris