Primitive

par **Anonyme** » 22 Jan 2006, 18:19

Bonjour,

J'ai un prob avec une primitive :
f(x)=(pi-|2x-pi|)sin(x))

On veut F (F étant la primitive de f) merci

par **tigri** » 22 Jan 2006, 18:48

bonsoir!
peux-tu dire l'ensemble donné par le texte comme ensemble de définition?
il faudrait peut-être écrire f(x) sans valeur absolue, selon certains intervalles, puis faire une intégration par parties

par **Anonyme** » 22 Jan 2006, 19:12

Salut,

L'énoncé :

Calculer l'intégrale

par **Anonyme** » 22 Jan 2006, 19:20

Re-

Elle est continue au-moins ? Parce que lorsque je visualise la fonction sur ma calculatrice je vois que des morceaux.

par **Anonyme** » 22 Jan 2006, 19:40

Personne ?

par **Mikou** » 22 Jan 2006, 19:56

la continuité par morceaux suffit.
Tu peux, si il ya besoin, commencer par eliminer la valeure absolue puis integrer par parties

par **Anonyme** » 22 Jan 2006, 20:07

C'est bien ca mon problème

par **Mikou** » 23 Jan 2006, 18:13

tu sais pas eliminer une valeure absolue ???

par **Galt** » 23 Jan 2006, 18:19

La fonction est clairement continue (une valeur absolue, c'est continu, un sinus aussi, une somme, un produit de fonctions continues)
Sur

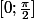
, tu as

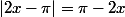
donc ...
Sur

,

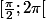
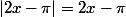
Puis Chasles et deux intégrations par parties

par **tigri** » 23 Jan 2006, 18:19

étudie le signe de 2x-pi et déduis-en les expressions de | 2x- pi| selon les intervalles

cf Galt ci-dessus

par **Mikou** » 23 Jan 2006, 18:20

Une suffit non ?

par **tigri** » 23 Jan 2006, 18:23

par Chasles tu as deux intégrales, chacune calculable avec une integration par parties

par **allomomo** » 23 Jan 2006, 20:35

Salut,

On note :

Si

,

donc

Si

,

donc

Calculons :

(Intégration par partie )

D'où :

Et :

En résumé :

Donc :

Primitive

Primitive

Qui est en ligne