Primitive introuvable
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
simluhuy
- Messages: 2
- Enregistré le: 14 Mar 2017, 20:00
-
par simluhuy » 14 Mar 2017, 20:05
Bonjour,
Je viens demander de l'aide car je ne parviens pas à trouver la primitive de la fonction suivante (qui doit pourtant être simple car elle vient du début de mon cours sur les primitives) :
 = \frac{e^{\frac{1}{x}}}{x^{2}})
Je ne sais pas à quelle forme m'en remettre
Merci pour votre aide
-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
par Lostounet » 14 Mar 2017, 20:08
simluhuy a écrit:Bonjour,
Je viens demander de l'aide car je ne parviens pas à trouver la primitive de la fonction suivante (qui doit pourtant être simple car elle vient du début de mon cours sur les primitives) :
Je ne sais pas à quelle forme m'en remettre
Merci pour votre aide
Salut,
En prenant u(x) = 1/x
Tu constates que u'(x) = -1/x^2
Et qu'on a donc ici la forme - (u'*exp(u))
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
simluhuy
- Messages: 2
- Enregistré le: 14 Mar 2017, 20:00
-
par simluhuy » 14 Mar 2017, 20:13
Ok merci c'est donc tout bête et je me retrouve avec
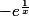
Merci
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 14 Mar 2017, 20:53
salut
 = \dfrac {e^{\frac 1 x}}{x^2} = - (- \dfrac 1 {x^2})e^{\frac 1 x})
et il suffit de regarder pour voir ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
