Prérequis et bases pour les futurs TS spé maths
17 messages
- Page 1 sur 1
Prérequis et bases pour les futurs TS spé maths
Bonsoir, j'ouvre ce topic à l'attention de tous ceux qui ont choisis la spécialité mathématiques en terminale.
Je me disais qu'on pourrais organiser à l'attention de tous les futurs TS spé maths une sorte de mini-prérequis où l'on réunirais les bases de l'arithmétique vu dans l'année pour ne pas arriver à la rentrée en spé complètement largué (je pense plus particulièrement à l'arithmétique qui représente quand même un peu plus de la moitié du programme annuel).
Si cela vous intéresse, n'hésitez pas à participer et à ajouter selon vous, les trucs à connaître, les réflexes, les érreurs à éviter, des résultats à connaîtres etc ...
Je me disais qu'on pourrais organiser à l'attention de tous les futurs TS spé maths une sorte de mini-prérequis où l'on réunirais les bases de l'arithmétique vu dans l'année pour ne pas arriver à la rentrée en spé complètement largué (je pense plus particulièrement à l'arithmétique qui représente quand même un peu plus de la moitié du programme annuel).
Si cela vous intéresse, n'hésitez pas à participer et à ajouter selon vous, les trucs à connaître, les réflexes, les érreurs à éviter, des résultats à connaîtres etc ...
Cool ! merci à vous
En référence à Lostounet, je n'y ai pas pensé mais tu peux aussi nous aidé étant donné qu'on voit un peu d'arithmétique en 3e et qu'on n'en revoit pas avant la terminale pour certains :++:
Je vais donc commencer par mettre deux, trois trucs de base.
Déjà, un peu de vocabulaire :
On dit que b divise a (noté b|a) ou que a est un multiple de b si et seulement si il existe un entier naturel q tel que a=bq.
exemple : 27 divise 81 ou 27|81 car
Nombre premier :
Un entier relatif a différent de -1, 1 et 0 et dit premier si et seulement si il n'est divisible que par 1, -1, a et -a.
Dans le cas d'un entier naturel b, il est dit premier si et seulement si il n'est divisible que par 1 et b.
exemple : -7 est premier car il n'est divisible que par 1, -1, 7 et -7.
19 est premier car il n'est divisible que par 1 et 19.
remarque :
- tout entier naturel a>1 admet au moins un diviseur premier
- tout entier naturel, non premier et strictement supérieur à 1, peut s'écrire d'une manière unique en un produit de facteurs premiers.
Décomposition en facteurs premiers :
Tout entier naturel N>1 admet une décompostion en facteurs premiers :

où est un nombre premier et
est un nombre premier et  pour
pour 
exemple :

PPCM et PGCD :
On appelle PPCM de deux ou plusieurs nombres (noté PPCM ou ) le plus petit commun multiple de deux ou plusieurs nombres.
) le plus petit commun multiple de deux ou plusieurs nombres.
Le PPCM est égal au produit de tous les facteurs premiers figurant dans chacun des nombre considérés, chacun étant affecté du plus grand des exposants avec lesquels il figure dans les nombres considérés.
exemple :
Le PPCM de 21 et 9 noté=21) ;)
;) se calcule en décomposant les entiers 9 et 21 :
se calcule en décomposant les entiers 9 et 21 :


Et donc=21) ;)
;)
Le calcul du PPCM peut servir pour trouver un dénominateur commun entre plusieurs fractions :
exemple : calculer :

On serait tenté de faire de grosses multiplications mais il y a plus simple :



=) 75;)81;)15
75;)81;)15

On appelle PGCD de deux ou plusieurs nombres (noté PGCD ou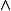 ) le plus grand commun multiple de deux ou plusieurs nombres.
) le plus grand commun multiple de deux ou plusieurs nombres.
Le PGCD est égal au produit des facteurs premiers commun à tous nombre considérés, chacun étant affecté du plus petit des exposants avec lesquels il figure dans les nombres considérés.
exemple :
Le PGCD de 21 et 9 noté=21\wedge 9) se calcule en décomposant les entiers 9 et 21 :
se calcule en décomposant les entiers 9 et 21 :


Et donc=21\wedge 9=3)
Le PGCD sert également à simplifier les quotient qui donneront un quotient irréductible, comme par exemple :

Le PGCD de 24 et 78 est 6 donc

Voilà, j'en reposterai demain, bonne nuit :+++:
En référence à Lostounet, je n'y ai pas pensé mais tu peux aussi nous aidé étant donné qu'on voit un peu d'arithmétique en 3e et qu'on n'en revoit pas avant la terminale pour certains :++:
Je vais donc commencer par mettre deux, trois trucs de base.
Déjà, un peu de vocabulaire :
On dit que b divise a (noté b|a) ou que a est un multiple de b si et seulement si il existe un entier naturel q tel que a=bq.
exemple : 27 divise 81 ou 27|81 car
Nombre premier :
Un entier relatif a différent de -1, 1 et 0 et dit premier si et seulement si il n'est divisible que par 1, -1, a et -a.
Dans le cas d'un entier naturel b, il est dit premier si et seulement si il n'est divisible que par 1 et b.
exemple : -7 est premier car il n'est divisible que par 1, -1, 7 et -7.
19 est premier car il n'est divisible que par 1 et 19.
remarque :
- tout entier naturel a>1 admet au moins un diviseur premier
- tout entier naturel, non premier et strictement supérieur à 1, peut s'écrire d'une manière unique en un produit de facteurs premiers.
Décomposition en facteurs premiers :
Tout entier naturel N>1 admet une décompostion en facteurs premiers :
où
exemple :
PPCM et PGCD :
On appelle PPCM de deux ou plusieurs nombres (noté PPCM ou
Le PPCM est égal au produit de tous les facteurs premiers figurant dans chacun des nombre considérés, chacun étant affecté du plus grand des exposants avec lesquels il figure dans les nombres considérés.
exemple :
Le PPCM de 21 et 9 noté
Et donc
Le calcul du PPCM peut servir pour trouver un dénominateur commun entre plusieurs fractions :
exemple : calculer :
On serait tenté de faire de grosses multiplications mais il y a plus simple :
On appelle PGCD de deux ou plusieurs nombres (noté PGCD ou
Le PGCD est égal au produit des facteurs premiers commun à tous nombre considérés, chacun étant affecté du plus petit des exposants avec lesquels il figure dans les nombres considérés.
exemple :
Le PGCD de 21 et 9 noté
Et donc
Le PGCD sert également à simplifier les quotient qui donneront un quotient irréductible, comme par exemple :
Le PGCD de 24 et 78 est 6 donc
Voilà, j'en reposterai demain, bonne nuit :+++:
Salut !
Je pense qu'on peut remettre le prog de 3ème , mais qu'on ne peut pas trop mordre sur celui de TS (même si c'est un approfondissement je vous l'accorde) , puisque sinon ce ne serait pas des prérequis, mais un cours.
( mon avis c'est que .. on a juste besoin de suivre correctement le début du cours d'arithmétique , et ce sans aucun prérequis )
Si j'ai le courage je mettrais quelque chose dans la semaine !
@dino : Tu va où l'année prochaine ?
Je pense qu'on peut remettre le prog de 3ème , mais qu'on ne peut pas trop mordre sur celui de TS (même si c'est un approfondissement je vous l'accorde) , puisque sinon ce ne serait pas des prérequis, mais un cours.
( mon avis c'est que .. on a juste besoin de suivre correctement le début du cours d'arithmétique , et ce sans aucun prérequis )
Si j'ai le courage je mettrais quelque chose dans la semaine !
@dino : Tu va où l'année prochaine ?
Quelque catégories de nombres remarquables
Nombre abondant : nombre inférieur à la somme de ses diviseurs propres.
ex : 12.
Nombres amiables : chacun est égal à la somme des diviseurs propres de l'autre.
ex : 220 et 284.
Nombre composé : nombre non premier, c'est-à-dire, qui admet plus de deux diviseurs.
ex : 35.
Nombre déficient : nombre supérieur à la somme de ses diviseurs propres.
ex : 8.
Nombres étrangers : deux nombres qui n'ont pas de diviseurs commun distincts de 1.
ex : 15 et 16.
Nombres hétérogènes : lorsque les ensembles de leurs facteurs premiers respectifs sont distincts.
ex : 14 et 21.
Nombres homogènes : lorsqu'ils admettent les mêmes facteurs premiers.
ex : 60 et 90.
Nombre parfait : nombre égal à la somme de ses diviseurs propres.
ex : 28.
Nombres premiers jumeaux : ce sont deux nombres premiers et consécutifs impairs.
ex : 3 et 5.
Nombre primaire : nombre qui est une puissance positive d'un nombre premier.
ex :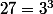 .
.
Nombre abondant : nombre inférieur à la somme de ses diviseurs propres.
ex : 12.
Nombres amiables : chacun est égal à la somme des diviseurs propres de l'autre.
ex : 220 et 284.
Nombre composé : nombre non premier, c'est-à-dire, qui admet plus de deux diviseurs.
ex : 35.
Nombre déficient : nombre supérieur à la somme de ses diviseurs propres.
ex : 8.
Nombres étrangers : deux nombres qui n'ont pas de diviseurs commun distincts de 1.
ex : 15 et 16.
Nombres hétérogènes : lorsque les ensembles de leurs facteurs premiers respectifs sont distincts.
ex : 14 et 21.
Nombres homogènes : lorsqu'ils admettent les mêmes facteurs premiers.
ex : 60 et 90.
Nombre parfait : nombre égal à la somme de ses diviseurs propres.
ex : 28.
Nombres premiers jumeaux : ce sont deux nombres premiers et consécutifs impairs.
ex : 3 et 5.
Nombre primaire : nombre qui est une puissance positive d'un nombre premier.
ex :
A part "étrangers" (qui est un terme qui ne s'utilise plus trop d'ailleurs, premiers entre eux est plus adéquat de nos jours) et "composé", les autres ne sont pas vraiment à connaitre.
Sinon, encore une fois, l'idée est bonne, mais à part vous, qui êtes déjà près pour la TS ou l'avez déjà terminée, personne ne risque de lire et de s'intéresser à ce topic.
Sinon, encore une fois, l'idée est bonne, mais à part vous, qui êtes déjà près pour la TS ou l'avez déjà terminée, personne ne risque de lire et de s'intéresser à ce topic.
Nightmare a écrit:Sinon, encore une fois, l'idée est bonne, mais à part vous, qui êtes déjà près pour la TS ou l'avez déjà terminée, personne ne risque de lire et de s'intéresser à ce topic.
C'est exactement ce pourquoi j'ai dit que ... ça n'était pas réellement utile ... :++:
Par contre, écrire un pdf avec tout ça , pourquoi pas, je trouverais l'idée bonne parce que un pdf c'est mieux qu'un thread et que ça fait quelque chose de concret !
Dinozzo13 a écrit:Quelque catégories de nombres remarquables
Nombre abondant : nombre inférieur à la somme de ses diviseurs propres.
ex : 12.
Nombres amiables : chacun est égal à la somme des diviseurs propres de l'autre.
ex : 220 et 284.
Nombre composé : nombre non premier, c'est-à-dire, qui admet plus de deux diviseurs.
ex : 35.
Nombre déficient : nombre supérieur à la somme de ses diviseurs propres.
ex : 8.
Nombres étrangers : deux nombres qui n'ont pas de diviseurs commun distincts de 1.
ex : 15 et 16.
Nombres hétérogènes : lorsque les ensembles de leurs facteurs premiers respectifs sont distincts.
ex : 14 et 21.
Nombres homogènes : lorsqu'ils admettent les mêmes facteurs premiers.
ex : 60 et 90.
Nombre parfait : nombre égal à la somme de ses diviseurs propres.
ex : 28.
Nombres premiers jumeaux : ce sont deux nombres premiers et consécutifs impairs.
ex : 3 et 5.
Nombre primaire : nombre qui est une puissance positive d'un nombre premier.
ex :.
Merci, je ne connaissais pas ces appellations !
17 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
