bonjour,
je vais te laisser faire une partie des démos :zen:
propriété (1)si f' et g' sont deux fonctions dérivées continues sur [0;x]
vérifiant[/I]
 > g'(t))
en intégrant sur l'intervalle [0;x] par rapport à la variable t, il vient:
-f(0) > g(x)-g(0))
indications pour démontrer ton résultaten appliquant une première fois la propriété (1) à
 > 1)
il vient
 > x)
si tu voulais intégrer à nouveau, tu ferais le changement de variable x=t.
Maintenant,posons:
=tan(x))
=x+\frac{1}{3}x^3+\frac{2}{15}x^5)
en utilisant la dérivée de u,
=1+tan^2(x)=(1+u^2(x)))
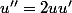
avec la formule de dérivée d'une fonction composée, on montre ainsi facilement que la dérivée troisième
}(x)=P(tan(x)))
où P est la fonction polynôme
=2+8X^2+6X^4)
la dérivée troisième de v est:
}(x)=2+8x^2)
on voit immédiatement que
}(t) > v^{(3)}(t))
pour
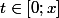
ensuite on primitive (on intégre) 3 fois cette inégalité sur
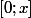
en faisant le changement de variable x=t entre deux intégrations successives.
on obtient le résultat demandé.
