Pourquoi cette égalité (intégrale)?

[Hardtoexplain91]

Bonjour, je ne comprends pas les 3 égalités suivantes:

Soit In =, appartient à ]0, et n appartient à N*.

1) Calculer In+In+2, en fonction de In+1.

Voilà je bloque ici, pourquoi on a cela:

In+2+In = = =

merci

[Sa Majesté]

Salut
On utilise
cos(a+b) + cos(a-b) = 2 cos a cos b
avec a=(n+1)t et b=t

cos((n+2)t) + cos(nt) = 2 cos((n+1)t) cos(t)

[Hardtoexplain91]

et le 2/sinalpha qui est sorti? on a multiplié par sinalpha/sinalpha c'est ça?

[Sa Majesté]

Oui c'est ça, c'est une astuce de calcul

[Hardtoexplain91]

pourquoi avons-nous : (-cos(n+1)t)dt +In+1 et pas (costsinalpha)dt+In+1 et pourquoi faire 1-1?....
merci

[Sa Majesté]

[Hardtoexplain91]

merci !

je dois calculer maintenant In... c'est la deuxième question.

Je trouve =.

Je dois désormais calculer In.

Donc = 0.
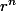
Je pose =In et r est différent de 0.
Donc on a :=0.
Et on a r²-=0

On a '= .

C'est quoi déjà la formule pour trouver ' s'il-vous-plaît?

Et la correction dit qu'il y a 2 cas: (je les mettrais après, je dois d'abord voir si j'obtiens le même ')

[Sa Majesté]

C'est



avec b'=b/2

[Hardtoexplain91]

je trouve (-4/sinalpha)² - 1 et pas 1/sin²alpha -1..

[Sa Majesté]

Mais non
b' = b/2 = 1/sin(alpha)
b'²-ac = 1/sin²(alpha) - 1 = cos²(alpha) / sin²(alpha)