Pour les amateurs des equations fonctionelles
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 06 Sep 2006, 23:47
par Oumzil » 06 Sep 2006, 23:47
texte de l'exercice :
determiez toutes les fontions f de IR+* vers IR et qui verifient :
f(x)f(y) = f(xy) + 1/x +1/y pour tous x et y de IR*
:++: à vous de jouer ! :mur: :marteau:
poste modifié !
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 00:40
par nekros » 07 Sep 2006, 00:40
Salut,
Bon, je me lance !
=\frac{x+1}{x}})
?
Pour
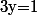
, on a :
f(1)=f(x)+\frac{1}{x}+1)
donc
(f(1)-1)=\frac{1}{x}+1)
soit
=\frac{\frac{1}{x}+1}{f(1)-1})
si
 \neq 1)
Or, pour
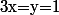
, on a :
)^2=f(1)+2)
soit
+1)(f(1)-2)=0)
donc soit
=-1)
soit
=2)
Pour
=-1)
,
)
n'est pas solution.
Pour
=2)
,
=\frac{x+1}{x})
est solution.
Sauf erreurs.
A+
-
Mahdi
- Membre Naturel
- Messages: 29
- Enregistré le: 12 Nov 2005, 13:36
-
 par Mahdi » 07 Sep 2006, 01:56
par Mahdi » 07 Sep 2006, 01:56
nekros a écrit:=\frac{x+1}{x})
oui c'est ça j'ai trouvé le meme resultat
=1+\frac{1}{x})
-
nekros
- Membre Irrationnel
- Messages: 1507
- Enregistré le: 30 Oct 2005, 18:57
-
 par nekros » 07 Sep 2006, 01:58
par nekros » 07 Sep 2006, 01:58
Ok, merci de confirmer :lol4:
-
Mahdi
- Membre Naturel
- Messages: 29
- Enregistré le: 12 Nov 2005, 13:36
-
 par Mahdi » 07 Sep 2006, 02:14
par Mahdi » 07 Sep 2006, 02:14
nekros a écrit:Ok, merci de confirmer :lol4:
Y'en a pas de quoi.
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 14:50
par Oumzil » 07 Sep 2006, 14:50
bravo !! :++: mais faut un peu détailler lol :error:
ma sollution diffère po dla tienne :soupir2:
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 15:01
par Flodelarab » 07 Sep 2006, 15:01
Oumzil a écrit: 1/x +1/y pour tous x et y de IR
Oumzil, tu peux pas t'empecher de diviser par 0 ! ... c plus fort que toi !
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:20
par Oumzil » 07 Sep 2006, 15:20
flodelarab ouvre grand les yeux
toutes les fontions f de IR+* vers IR
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:21
par Oumzil » 07 Sep 2006, 15:21
tu vois l'etoile non ? :ptdr:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 15:23
par nox » 07 Sep 2006, 15:23
Oui mais tu l'as oubliée ici

Oumzil a écrit: f(x)f(y) = f(xy) + 1/x +1/y pour tous x et y de IR
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 15:24
par Flodelarab » 07 Sep 2006, 15:24
Apparemment j'ouvre les yeux plus grand que toi.
Mais bon ... c pas moi ki ai écrit le message ...
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:26
par Oumzil » 07 Sep 2006, 15:26
Flodelarab a écrit:Oumzil, tu peux pas t'empecher de diviser par 0 ! ... c plus fort que toi !
c'est bien ton pseudo non ?
-
Flodelarab
- Membre Légendaire
- Messages: 6574
- Enregistré le: 29 Juil 2006, 14:04
-
 par Flodelarab » 07 Sep 2006, 15:30
par Flodelarab » 07 Sep 2006, 15:30
Oumzil a écrit:c'est bien ton pseudo non ?
c pas moi ki est écrit le message fautif
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 15:35
par haydenstrauss » 07 Sep 2006, 15:35
Oumzil a écrit:texte de l'exercice :
determiez toutes les fontions f de IR+* vers IR et qui verifient :
f(x)f(y) = f(xy) + 1/x +1/y pour tous x et y de IR
:++: à vous de jouer ! :mur: :marteau:
C'est cntradictoire tu dis:
"fontions f de IR+* vers IR "
et apres tu dis :
"pour tous x et y de IR"
il aurait fallu mettre
pour tous x et y de IR+*
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:35
par Oumzil » 07 Sep 2006, 15:35
:briques: :ptdr: :marteau: :happy2: :ptdr:
-
nox
- Membre Complexe
- Messages: 2157
- Enregistré le: 14 Juin 2006, 09:32
-
 par nox » 07 Sep 2006, 15:36
par nox » 07 Sep 2006, 15:36
il n'est pas la pour l'instant...
pourquoi veux tu fermer cette discussion ?
apparemment tu as encore des problemes avec la notion d'ensemble de définition. Pourquoi tu ne veux pas qu'on te l'explique ?
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:37
par Oumzil » 07 Sep 2006, 15:37
nekros tu vois encore ce qui se passe :marteau: ils jouent les idiots encore
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 15:38
par haydenstrauss » 07 Sep 2006, 15:38
Oumzil te vexe pas tu passe en terminal sa fait que un ou deux ans que tu vois ça je passe en premiere année de fac moi aussi je fait des erreurs.
J'aime meme demander a ce qui ont me demontre que le perimetre d'un cercle fasse 2 pi
Et ça ma pris bcp de temps pour comprendre ...
-
Oumzil
- Membre Relatif
- Messages: 412
- Enregistré le: 03 Sep 2006, 21:38
-
 par Oumzil » 07 Sep 2006, 15:39
par Oumzil » 07 Sep 2006, 15:39
nox c'est juste hier j'ai demandé à un prof il m'a dit que si tu pose la condition IR+ vers IR* tu peux écrire f(x) = .. pour tout x de IR puisque la condition de l'ensemble de définition vient avant . mais flodelarab essaye de me vexer à chaque fois qu'il peut
-
haydenstrauss
- Membre Relatif
- Messages: 378
- Enregistré le: 11 Juil 2006, 10:19
-
 par haydenstrauss » 07 Sep 2006, 15:40
par haydenstrauss » 07 Sep 2006, 15:40
nekros a écrit:Salut,
Bon, je me lance !
=\frac{x+1}{x}})
?
Pour
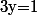
, on a :
f(1)=f(x)+\frac{1}{x}+1)
donc
(f(1)-1)=\frac{1}{x}+1)
soit
=\frac{\frac{1}{x}+1}{f(1)-1})
si
 \neq 1)
Or, pour
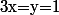
, on a :
)^2=f(1)+2)
soit
+1)(f(1)-2)=0)
donc soit
=-1)
soit
=2)
Pour
=-1)
,
)
n'est pas solution.
Pour
=2)
,
=\frac{x+1}{x})
est solution.
Sauf erreurs.
A+
Comment tu as fait pour trouver? Par intuitions ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 112 invités
