DM POUR DEMAIN AIder moi

[lefrere9]

Bonjour à tous je suis bloqué je cherche à savoir comment on trouve les coordonnés et l'équation d'une tangente parallèle a une autre tangente dont on connait l'équation
Merci de m'aider

[Sa Majesté]

Évidemment quand on se réveille le dimanche soir à 18h20, c'est un peu dur ...
Si tu connais une première tangente, alors tu connais son coefficient directeur
Or 2 droites parallèles ont le même coef directeur
Et le coef directeur c'est la valeur de la dérivée en l'abscisse du point considéré

[lefrere9]

Lool nn j'ai commencé depuis et à chaque fois j'arrive pas a faire les 2zièmes questions oui voilà l'équation de la 1ere tangente est Y=-4x+3
donc coef directeur est de -4 après je sais que je dois faire Y=-4 une truc comme ça mais j'arrive pas à résoudre
Merrci

[Sa Majesté]

Poste tout ton exo parce que là c'est difficile à suivre

[lefrere9]

ok donc;: Soit la fontion ff définie sur R\{1,5} par f(x)= x²/2x-3

1.Determiner une équation de la tangente T à la courbe C representative de F au Point d'abcisse 1.
Resultat :j'ai trouvé Y=-4x+3

2.Existe t-il un autre point de la courbe C pour lequel la tangente à C est parallele à T?? Si oui determiner ses coordonnées et une équation de cette seconde tangente.

voilà Dsl du retard merci

[Sa Majesté]

La tangente au point d'abscisse x0 a pour coefficient directeur f'(x0)
Pour que cette tangente soit parallèle à la droite d'équation y=-4x+3, il faut que f'(x0) soit égal à -4

[lefrere9]

Ok ça suppose que je dois calculé f'(o) mais je trouve x ??

[Sa Majesté]

Ok ça suppose que je dois calculé f'(o) mais je trouve x ??

:briques:

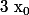
c'est l'abscisse du point

[lefrere9]

lol oulà les x0 là ça devient compliqué après je ne trouve pas 4 le coef directeur in qu'est que t'en pense

[gigamesh]

Salut,
tu cherches tel que .
Bah tu résous l'équation !
L'égalité est une équation d'inconnue ;
ça se voit mieux en utilisant l'expression de que tu as du trouver précédemment :
se réécrit

[lefrere9]

Salut,
tu cherches tel que .
Bah tu résous l'équation !
L'égalité est une équation d'inconnue ;
ça se voit mieux en utilisant l'expression de que tu as du trouver précédemment :
se réécrit

Merci j'avais pas vu votre réponse wi donc j'ai fais tout ça mais j'arrive pas je crois mon problème il fait que je reprenne tout à zéro résultion d'équation ect...parce que à mm en posant ça {2x_0^2-6x_0}{(2x_0-3)^2}=4
j'arrive pas à démarer merci

[gigamesh]

Hum...

truc sur machin = 4 c'est pareil que truc = 4 * machin
tu sais pas résoudre les équations de second degré ?