Polynomes =S

[laurie26500]

bonjours voila c'est assez important, je narrive pas a faire cet exercice :


on considere l'hyperbole H d'équation y=x/2et les droites Dm d'équation :
y= m(x+1) -2

1) verifier que les droites Dm passent par un point fixe C, indépendant de m, et que C appartient a H.

2) determiner le réel m de telle sorte que Dm et H aient seulement le point C en commun.

et une ptite question a part : comment factoriser le polynome : -6x² - 3x -3

je vous remercie davance =)

[aeon]

y=x/2 n'est pas une hyperbole...

[Luc]

Salut,

bonjours voila c'est assez important, je narrive pas a faire cet exercice :


on considere l'hyperbole H d'équation y=x/2

L'équation de H est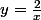 , pas 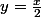qui est l'équation d'une droite.

1) verifier que les droites Dm passent par un point fixe C, indépendant de m, et que C appartient a H.

Trace D_1 et D_2 et regarde leur point d'intersection. C'est C.
Essaye alors de montrer que toutes les droites Dm passent par C (c'est-à-dire que pour tout m, , et que C appartient à H, c'est-à-dire que .

et une ptite question a part : comment factoriser le polynome : -6x² - 3x -3

Mets -6 en facteur. Après tu auras x^2-1/2x - 1/2. L'astuce de la forme canonique est de dire que x^2-1/2x est le début d'un carré:(x-1/4)^2 - ...
Tu auras alors une identité remarquable du type a^2-b^2 que tu pourras factoriser.

Bons calculs,
Luc

[laurie26500]

ah wii pardon l'hyperbole est 2/x
excuse moi luc, mais je ne comprends pas tout ce que tu dis come on vient de commencer cette leçon , esque tu pourrait approffondire un peu ? sil te plait
merci =)

[Luc]

ah wii pardon l'hyperbole est 2/x
excuse moi luc, mais je ne comprends pas tout ce que tu dis come on vient de commencer cette leçon , esque tu pourrait approffondire un peu ? sil te plait
merci =)

Ok, mais qu'est-ce que tu ne comprends pas? Est-ce que tu arrives à tracer D1 et D2 ?

Luc

[laurie26500]

c'est pour remplacer les expressions littéraires par des chiffres =S

et pour le polynôme -6x²-3x-3 , j'ai beau essayé de le factoriser pour ensuite le mettre sous un tableau de signe, je n'y arrive pas !!

[Luc]

c'est pour remplacer les expressions littéraires par des chiffres =S

et pour le polynôme -6x²-3x-3 , j'ai beau essayé de le factoriser pour ensuite le mettre sous un tableau de signe, je n'y arrive pas !!

Trace D1 et D2:

D1 est la droite d'équation y= m(x+1) -2 en remplaçant m par 1.
C'est à dire d'équation y= x + 1 - 2 = x - 1

D2 est la droite d'équation y= m(x+1) -2 en remplaçant m par 2.
C'est à dire d'équation y= 2(x + 1) - 2 = 2x +2 - 2 = 2x

Quel est l'intersection de D1 et D2?

Quelle est l'équation de D3 ? de D0 ? (pour voir si tu as compris).

Luc

[laurie26500]

et bien pour D0 et D3 on remplace m par 0 pour la premiere et par 3 pour la deuxieme ?
sur la calculette je vois bien ou est le point d'intersection mais sans je ne sais pas faire :triste:

[Luc]

et bien pour D0 et D3 on remplace m par 0 pour la premiere et par 3 pour la deuxieme ?

Oui c'est bien ça!

Donc que sont les équations que tu obtiens pour D0 et D3 ?

Luc

[laurie26500]

et ben 3( x + 1 )-2 = 3x+3-2= 3x +1

et : 0 ( x+ 1 )-2 = -2 ???? ^^

[Luc]

Oui c'est bien ça mais attention à ne pas oublier y= ...:

Donner l'équation d'une droite, c'est dire que pour tous les points de coordonnées (x,y) sur la droite, on peut écrire

y=ax+b et a et b sont les mêmes pour tous les points sur la droite!

Ici l'équation de D0 est y=-2.
L'équation de D3 est y = 3x +1

Luc

[laurie26500]

Oula mais alors ça sert a quoi D0 et D3
je comprends pas =S jsuis vraiment nulle :marteau:
a c'est pour prouver que ça a la meme intersection mais apre sje le prouve par des calculs ou avec le graphique ? parce que par des claculs je vois pas la

en tout cas merci de ton aide =)

[Luc]

Rebonsoir,

D0 et D3 c'était juste pour te faire comprendre que les droites Dm se coupent en un même point. Mais pour autant, on ne l'a pas encore démontré. Il faut le démontrer mathématiquement.

Il faut donc prouver par le calcul que toutes les droites Dm se coupent en un même point, puisqu'on ne peut pas dessiner une infinité de droites ...

Il faut montrer par le calcul que le point C que tu as trouvé appartient à toutes les droites Dm. Que valent les coordonnées de C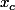 et ?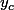

Méthode: Tu montres que vérifie l'équation pour tout m.

Bons calculs,

Luc

PS: On n'est pas nul(le) en maths si on persévère et qu'on demande ce qu'on ne comprend pas!