Polynômes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Juil 2010, 10:35
par girdav » 25 Juil 2010, 10:35
D'ailleurs, pour revenir au 2 on peut faire une petite généralisation :

est un polynôme à coefficients entiers qui prend la valeur

en 3 entiers et on montre qu'il ne prend la valeur
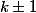
en aucun autre entier.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 25 Juil 2010, 10:36
par Dinozzo13 » 25 Juil 2010, 10:36
Ca m'aiderait beaucoup si tu pouvais m'éclairer :we:

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Juil 2010, 10:40
par Ben314 » 25 Juil 2010, 10:40
Nightmare a écrit:Essaye d'examiner les racines éventuelles de P.
Tient, perso, j'ai pas fait comme ça...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Anonyme
 par Anonyme » 25 Juil 2010, 10:50
par Anonyme » 25 Juil 2010, 10:50
Si P(x) a une racine alors il en a une infinité.
-
Anonyme
 par Anonyme » 25 Juil 2010, 10:57
par Anonyme » 25 Juil 2010, 10:57
donc P(x)=k=cte ? car pour moi il n'y a pas de polynôme avec une infinité de racine.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Juil 2010, 11:01
par girdav » 25 Juil 2010, 11:01
Pour le 3 on peut considérer la fraction rationnelle
}{P(X)})
qui est périodique.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Juil 2010, 11:19
par Nightmare » 25 Juil 2010, 11:19
Qmath a écrit:Si P(x) a une racine alors il en a une infinité.
Effectivement, mais ce n'est pas si immédiat.
Girdav a écrit: Pour le 3 on peut considérer la fraction rationnelle
}{P(X)})
qui est périodique.
C'est ce que j'ai fait originellement, la preuve par les racines me semble un peu plus "naturelle" pour les lycéens.
-
Anonyme
 par Anonyme » 25 Juil 2010, 11:29
par Anonyme » 25 Juil 2010, 11:29
Nightmare a écrit:Effectivement, mais ce n'est pas si immédiat.
??
Si P(x) admet une racine

alors
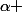
1 ou
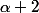
est une racine donc lexistence d'une racine entraîne lexistence d'une autre différente de la première donc une infinité .
C'est pas assez rigoureux ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Juil 2010, 11:40
par Nightmare » 25 Juil 2010, 11:40
Il y a des choses à écrire pour conclure que l'ensemble des zéros est infini. Effectivement, si z est racine, z+1 ou z+2 l'est aussi. Par récurrence, on a donc pour tout n que z+n ou z+n+1 ou ... ou z+2n est racine. Le problème est qu'il faut que les ensembles des z+p soient disjoints. Pour ça, on peut prendre
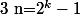
par exemple.
Dans ce cas, les ensembles
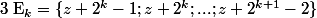
sont tous deux à deux disjoints (k variant) ce qui permet de conclure que Z est infini.
-
Anonyme
 par Anonyme » 25 Juil 2010, 11:44
par Anonyme » 25 Juil 2010, 11:44
Nightmare a écrit:Il y a des choses à écrire pour conclure que l'ensemble des zéros est infini. Effectivement, si z est racine, z+1 ou z+2 l'est aussi. Par récurrence, on a donc pour tout n que z+n ou z+n+1 ou ... ou z+2n est racine. Le problème est qu'il faut que les ensembles des z+p soient disjoints. Pour ça, on peut prendre
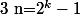
par exemple.
Dans ce cas, les ensembles
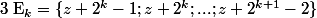
sont tous deux à deux disjoints (k variant) ce qui permet de conclure que Z est infini.
L'es racines sont distinctes car on peut montrer par recurrence que la relation d'ordre entre les racines est stricte ( > ou < )
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Juil 2010, 11:47
par girdav » 25 Juil 2010, 11:47
Une autre idée consiste à montrer que pour tout entier

on a
P(X+2)=P(X)P(X+n+3))
. On voit alors que si

est racine on a que pour tout entier

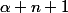
ou
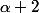
sont racines. On en déduit que
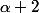
est racine.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Juil 2010, 11:55
par Nightmare » 25 Juil 2010, 11:55
Qmath a écrit:L'es racines sont distinctes car on peut montrer par recurrence que la relation d'ordre entre les racines est stricte ( > ou < )
Je n'ai pas trop compris ceci...
Autre chose au passage, notre raisonnement demande à ce que P ait au moins une racine! Donc il y a autre chose à préciser.
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 25 Juil 2010, 12:00
par Doraki » 25 Juil 2010, 12:00
Il dit que pour toute racine a, il existe une racine b avec aCe qui assure l'existence d'une infinité de racines dès qu'on en trouve une.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Juil 2010, 12:08
par Nightmare » 25 Juil 2010, 12:08
Ok, ça me va. La méthode proposée par Girdav est tout de même la plus élégante.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 25 Juil 2010, 12:18
par Ben314 » 25 Juil 2010, 12:18
Comme un polynôme non constant admet un nombre fini non vide de racines sur C, on peut aussi prendre celle de plus grande partie réelle. Comme P(z)=0 implique P(z+1) ou P(z+2)=0, on tombe sur une contradiction.
P.S. ma première méthode était :
Si P est non identiquement nul alors, pour "presque tout" z, on a
}{P(z+1)}=\frac{P(z+2)}{P(z+3)}=\frac{P(z+4)}{P(z+5)}=...=\frac{P(z+2n)}{P(z+2n+1)}=...=1)
en faisant n->oo
Donc
=P(z))
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Anonyme
 par Anonyme » 25 Juil 2010, 16:07
par Anonyme » 25 Juil 2010, 16:07
Pour revenir a la resolution:
P(x) admet une racine ===> P(x) =0
P(x) n'admet pas de racine ===> P(x)= k ou P(x)= ??
Comment continuer dans le cas ou P(x) n'a pas de racine ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 25 Juil 2010, 16:25
par Nightmare » 25 Juil 2010, 16:25
Est-ce vraiment possible que P n'ait pas de racines?
-
Anonyme
 par Anonyme » 25 Juil 2010, 16:39
par Anonyme » 25 Juil 2010, 16:39
Nightmare a écrit:Est-ce vraiment possible que P n'ait pas de racines?
P(x)=k k different de 0
Dans le cas ou P est un polynôme non constant c'est tres peu probable que P n'ai pas de racine ( Pour ne pas dire je suis sur que P admet des racines). Mais il me manque des preuves. Je réfléchi ...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 25 Juil 2010, 16:41
par girdav » 25 Juil 2010, 16:41
Qmath a écrit:P(x)=k k different de 0
Dans le cas ou P est un polynôme non constant c'est tres peu probable que P n'ai pas de racine ( Pour ne pas dire je suis sur que P admet des racines). Mais il me manque des preuves. Je réfléchi ...
Ici

est à coefficients complexes, donc par le théorème de d'Alembert-Gauß (ou théorème fondamental de l'algèbre) si

n'est pas constant il admet au moins une racine.
-
Anonyme
 par Anonyme » 25 Juil 2010, 16:46
par Anonyme » 25 Juil 2010, 16:46
Maintenant que tu le dis ...
Au fait polynôme complexe = coefficient complexe + domaine = C ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 67 invités
qui est périodique.
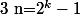 par exemple.
par exemple.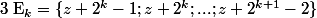 sont tous deux à deux disjoints (k variant) ce qui permet de conclure que Z est infini.
sont tous deux à deux disjoints (k variant) ce qui permet de conclure que Z est infini.par exemple.
sont tous deux à deux disjoints (k variant) ce qui permet de conclure que Z est infini.
}{P(z+1)}=\frac{P(z+2)}{P(z+3)}=\frac{P(z+4)}{P(z+5)}=...=\frac{P(z+2n)}{P(z+2n+1)}=...=1) en faisant n->oo
en faisant n->oo=P(z))
