Polynomes première S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 11 Nov 2013, 13:19
par koddo » 11 Nov 2013, 13:19
exercice1: Soit un polynôme. On pose Q(x)=P(x)+1 . Démontrer que [ P(x)]^2n+[Q(x)]^2+1 est divisible par P(x)Q(x).

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 11 Nov 2013, 15:23
par capitaine nuggets » 11 Nov 2013, 15:23
koddo a écrit:exercice1: Soit un polynôme. On pose Q(x)=P(x)+1 . Démontrer que [ P(x)]^2n+[Q(x)]^2+1 est divisible par P(x)Q(x).
Remplace le 1 de ton expression par 1=Q(x)-P(x).
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 13 Nov 2013, 14:35
par koddo » 13 Nov 2013, 14:35
capitaine nuggets a écrit:Remplace le 1 de ton expression par 1=Q(x)-P(x).
Excusez moi j'ai commis une erreur sur l'énoncé:En réalité l'exercice est le suivant:
Soit P(x) un polynome ;on pose Q(x)=P(x)+1.Démontre que P(x)^2n + Q(x)^n -1 est divisible par P(x)Q(x)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 13 Nov 2013, 15:09
par chan79 » 13 Nov 2013, 15:09
koddo a écrit:Excusez moi j'ai commis une erreur sur l'énoncé:En réalité l'exercice est le suivant:
Soit P(x) un polynome ;on pose Q(x)=P(x)+1.Démontre que P(x)^2n + Q(x)^n -1 est divisible par P(x)Q(x)
Montre que
^{2n}+(P(x)+1)^n -1)
est divisible par P(x) (les 1 se simplifient si on développe
+1)^n -1)
ensuite montre que
^{2n}+(P(x)+1)^n -1)
est divisible par
 +1)
(transforme
^{2n} -1))
P et Q sont-ils premiers entre eux ?
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 13 Nov 2013, 16:21
par koddo » 13 Nov 2013, 16:21
Voila ce que j'ai fait: On a:On a : [HTML]On a : Q(x)=P(x)+1 donc 1=P(x)-Q(x)
Ce qui donne P(x)^2n+Q(x)^n -1= P(x)^2n+Q(x)^n -P(x)+Q(x) puis je factorise par P(x)Q(x) et jobtiens
P(x)Q(x)[P(x)^2n-1Q(x)^-1+P(x)^-1Q(x)^n-1+Q(x)^-1-P(x)^-1]
[/PHP] [/HTML]
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 13 Nov 2013, 16:25
par koddo » 13 Nov 2013, 16:25
On a : Q(x)=P(x)+1 donc 1=P(x)-Q(x)
Ce qui donne P(x)^2n+Q(x)^n -1= P(x)^2n+Q(x)^n +P(x)-Q(x) puis je factorise par P(x)Q(x) et jobtiens
P(x)Q(x)[P(x)^2n-1Q(x)^-1+P(x)^-1Q(x)^n-1-Q(x)^-1+P(x)^-1]
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 14 Nov 2013, 13:23
par koddo » 14 Nov 2013, 13:23
chan79 a écrit:Montre que
^{2n}+(P(x)+1)^n -1)
est divisible par P(x) (les 1 se simplifient si on développe
+1)^n -1)
ensuite montre que
^{2n}+(P(x)+1)^n -1)
est divisible par
 +1)
(transforme
^{2n} -1))
P et Q sont-ils premiers entre eux ?
pour la première question on a P(x)^2n+(P(x)+1)^n+1=P(x)^n+nP(x)^n-1+...+1-1 est divisble par P(x).
Mais pour la deuxième voila ce j'obtiens: après transformation (P(x)^n+1)(P(x)^n-1)+(P(x)+1)^n
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 14 Nov 2013, 23:43
par koddo » 14 Nov 2013, 23:43
chan79 a écrit: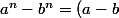( \ ...\ ))
^{2n}-1=(P(x)^2)^n -1^n =((P(x)^2-1)( \ ...\ )=(P(x)+1)(P(x-1)( \ ...\ ))
P(x)2n+Q(x)n -1= (P(x)+1)(P(x)-1)(
)+(P(x)+1)(P(x)+1)^n-1 qui est divisible par P(x)+1 donc par Q(x)
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 14 Nov 2013, 23:52
par koddo » 14 Nov 2013, 23:52
voici un autre exercice qui me pose problème:
n étant un entier naturel on désigne par fn le polynôme défini par :
f (x) =nx^n+1 - (n+1)x^n +1
Démontrer quil existe un polynôme gn tel que, pour tout réel x :
f (x)= (x-1)^2 gn (x)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Nov 2013, 07:25
par chan79 » 15 Nov 2013, 07:25
koddo a écrit:voici un autre exercice qui me pose problème:
n étant un entier naturel on désigne par fn le polynôme défini par :
f (x) =nx^n+1 - (n+1)x^n +1
Démontrer quil existe un polynôme gn tel que, pour tout réel x :
f (x)= (x-1)^2 gn (x)
si un polynôme est divisible par P et Q, est-il obligatoirement divisible par PQ ?
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 15 Nov 2013, 13:21
par koddo » 15 Nov 2013, 13:21
chan79 a écrit:si un polynôme est divisible par P et Q, est-il obligatoirement divisible par PQ ?
Il faut que P et Q soient premiers entre eux je crois bien

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Nov 2013, 14:17
par chan79 » 15 Nov 2013, 14:17
koddo a écrit:Il faut que P et Q soient premiers entre eux je crois bien
oui, et est-ce que c'est vrai ici ?
-
koddo
- Membre Naturel
- Messages: 54
- Enregistré le: 05 Nov 2011, 16:35
-
 par koddo » 15 Nov 2013, 14:27
par koddo » 15 Nov 2013, 14:27
chan79 a écrit:oui, et est-ce que c'est vrai ici ?
Deux polynomes Pet Q sont Premiers entre eux s'il existe deux polynomes U et V tels que
PU+QV=1 si on pose ici U=-1 et V=1 avec Q=P+1 On verra bien P et Q sont premiers entre eux

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 15 Nov 2013, 17:34
par chan79 » 15 Nov 2013, 17:34
koddo a écrit:Deux polynomes Pet Q sont Premiers entre eux s'il existe deux polynomes U et V tels que
PU+QV=1 si on pose ici U=-1 et V=1 avec Q=P+1 On verra bien P et Q sont premiers entre eux
On est d'accord ! :zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités

est divisible par P(x) (les 1 se simplifient si on développe
est divisible par
(transforme
