Pôlynome de Tchebychev
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
alexis6
- Membre Relatif
- Messages: 273
- Enregistré le: 13 Oct 2014, 12:32
-
 par alexis6 » 11 Jan 2016, 19:45
par alexis6 » 11 Jan 2016, 19:45
Bonsoir,
Dans un exercice, on pose:
=1 ; U(1)=2X, U(n+2)=2XU(n+1)-U(n))
On demande de montrer d'abord que pour tout complexe z different de 0,1,-1
( \frac{ z + \frac{1}{z}}{2} ) = \frac{z^{n+1} - \frac{1}{ z^{n+1}}}{z-\frac{1}{z}})
Mais je trouve que cette formule est fausse...
Je presice qu'il n'est pas dit dans l'execice sur quelle partie de N on doit démontrer ça.
merci
La modestie s'apprend par la répétition de l'échec.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 11 Jan 2016, 20:48
par Ben314 » 11 Jan 2016, 20:48
Salut,
Qu'est-ce qui te fait penser que c'est faux ?
Perso., il me semble bien que c'est parfaitement correct pour tout
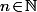
et tout
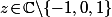
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
alexis6
- Membre Relatif
- Messages: 273
- Enregistré le: 13 Oct 2014, 12:32
-
 par alexis6 » 12 Jan 2016, 00:09
par alexis6 » 12 Jan 2016, 00:09
Ben314 a écrit:Salut,
Qu'est-ce qui te fait penser que c'est faux ?
Perso., il me semble bien que c'est parfaitement correct pour tout
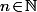
et tout
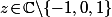
Pour n=0
(z+1/z)/2=1 --> (z-1)^2=0 --> z=1 donc pour 0 c'est faux
j'ai testé pour n=2 et n=3 ça fait le même style de résultats
La modestie s'apprend par la répétition de l'échec.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Jan 2016, 17:11
par Ben314 » 13 Jan 2016, 17:11
alexis6 a écrit: Ben314 a écrit:Pour n=0
(z+1/z)/2=1 --> (z-1)^2=0 --> z=1 donc pour 0 c'est faux
j'ai testé pour n=2 et n=3 ça fait le même style de résultats
Qu'est ce que c'est que ces salades que tu m'écrit là.
Je comprend franchement pas d'où tu a bien pu sortir ta relation
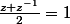
(d'un chapeau ?)
Ce que tu doit montrer, c'est que, pour tout
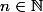
et tout
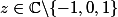
on a
=\frac{z^{n+1}-z^{-n-1}}{z-z^{-1}})
.
Pour

, on a
=U_0\big(\frac{z+z^{-1}}{2}\big)=1\)
vu que l'énoncé te dit que
\!=\!1)
pour tout

.
Et d'un autre coté, si

, on a

Donc le résultat est tout ce qu'il y a de plus vrai pour

.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
alexis6
- Membre Relatif
- Messages: 273
- Enregistré le: 13 Oct 2014, 12:32
-
 par alexis6 » 13 Jan 2016, 21:22
par alexis6 » 13 Jan 2016, 21:22
Bonsoir... Merci de m'avoir remis sur le bon chemin! Je voyais U(0)(z+z^-1)/2 non par comme une fonction f(x), mais comme un produit... Donc c'est sur à partir de là... Les notations de l'exercice m'ont induites en erreur. On pouvoit croire que U(n)(z+z-1)/2 était le produit du polynome U(n) ( donc par exemple pur 0, 1 ) fois le complexe ci dessus.
La modestie s'apprend par la répétition de l'échec.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 13 Jan 2016, 23:37
par Ben314 » 13 Jan 2016, 23:37
Effectivement, vu comme ça, ça risquait pas de marcher....
Mais d'un autre coté, si ça avait été un produit, je vois franchement pas ce qu'aurais puis signifier le X de
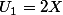
et de la formule de récurrence (qui te disait clairement que les
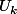
sont des polynômes en la variable X)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
alexis6
- Membre Relatif
- Messages: 273
- Enregistré le: 13 Oct 2014, 12:32
-
 par alexis6 » 14 Jan 2016, 19:23
par alexis6 » 14 Jan 2016, 19:23
Certes, mais on aurait pu mètre n en indice pour plus de clareté. Merci en tous cas.
La modestie s'apprend par la répétition de l'échec.
-
alexis6
- Membre Relatif
- Messages: 273
- Enregistré le: 13 Oct 2014, 12:32
-
 par alexis6 » 16 Jan 2016, 00:47
par alexis6 » 16 Jan 2016, 00:47
Finalement avec les explications de Ben j'ai réussi à démontrer les propriétés ( j'ai fait de même pour les polynômes de Tchebychev de première espèce ). J'aimerais savoir à quoi servent ces polynômes, ou du moins si ils ont une utilité.

La modestie s'apprend par la répétition de l'échec.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Jan 2016, 01:22
par Ben314 » 16 Jan 2016, 01:22
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
et tout