Polynôme
14 messages
- Page 1 sur 1
Polynôme
Bonjour,
Je suis en train de faire un DM de maths, mais je bloque partiellement sur une question.
"Une entreprise fabrique entre 0 et 1000 objets par mois. Le bénéfice en k de cette entreprise pour la fabrication de x centaines d'objets est donné par :
B(x) = 4x3(au cube, je ne sais pas faire d'exposant)-7x²+8x-3"
Pour quelles quantités d'objets fabriqués le bénéfice est-il positif ou nul ?
Alors, je pense que le bénéfice est nul quand x = 1 (soit 100 objets) et donc positif ou nul de 1 à +infini seulement je ne sais pas du tout comment rédiger et justifier ma réponse. Merci de m'aider.
Isaac
Je suis en train de faire un DM de maths, mais je bloque partiellement sur une question.
"Une entreprise fabrique entre 0 et 1000 objets par mois. Le bénéfice en k de cette entreprise pour la fabrication de x centaines d'objets est donné par :
B(x) = 4x3(au cube, je ne sais pas faire d'exposant)-7x²+8x-3"
Pour quelles quantités d'objets fabriqués le bénéfice est-il positif ou nul ?
Alors, je pense que le bénéfice est nul quand x = 1 (soit 100 objets) et donc positif ou nul de 1 à +infini seulement je ne sais pas du tout comment rédiger et justifier ma réponse. Merci de m'aider.
Isaac
Ah, oui, je suis allé un peu trop vite
Et si on essayait de la dériver? Si on a de la chance, on aura une fonction monotone, et alors, il nous suffira de trouver, avec une équation, en quelle valeur elle s'annule, il ne restera plus qu'à préciser qu'elle est négative avant et positive après si elle est croissante, ou le contraire, si elle est décroissante
Un conseil: utilise Géogébra (par exemple) pour voir à qui tu as affaire :we:
Et si on essayait de la dériver? Si on a de la chance, on aura une fonction monotone, et alors, il nous suffira de trouver, avec une équation, en quelle valeur elle s'annule, il ne restera plus qu'à préciser qu'elle est négative avant et positive après si elle est croissante, ou le contraire, si elle est décroissante
Un conseil: utilise Géogébra (par exemple) pour voir à qui tu as affaire :we:
Bon, j'explique ma démarche quand même, car ça fait un peu trop "identité qui sort de mon chapeau magique".
L'idée est de réécrire l'expression sous la forme^3 + b(wx + y)^2 + c)
avec des réels à déterminer, avec
des réels à déterminer, avec 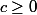 , puisqu'à partir de là, on a
, puisqu'à partir de là, on a ^3 + b(wx + y)^2 + c \geq a(ux-v)^3) , dont le signe de ce dernier est très facile à donner.
, dont le signe de ce dernier est très facile à donner.
)
Je reconnais ici un polynôme (dans la parenthèse) de la forme^3 = x^3 + 3a^2 + 3a + a^3) . Sauf qu'on voit que tous les coefficients ne sont pas liés, donc on ne peut trouver un tel
. Sauf qu'on voit que tous les coefficients ne sont pas liés, donc on ne peut trouver un tel  , d'où l'idée "d'approcher" ce polynôme. J'essaye de travailler avec des entiers. Comme on a -3/4,
, d'où l'idée "d'approcher" ce polynôme. J'essaye de travailler avec des entiers. Comme on a -3/4,  doit être négatif. Comme le premier entier > 3/4 est 1, j'essaye de développer ceci :
doit être négatif. Comme le premier entier > 3/4 est 1, j'essaye de développer ceci :
^3 = x^3 - 3x^2 + 3x - 1)
Or moi je veux arriver à :
:
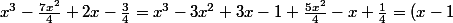^3 + \frac{5x^2}{4} - x + \frac{1}{4})
^3 + (x^2 - x + \frac{1}{4}) + \frac{x^2}{4})
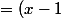^3 + (x-\frac{1}{2})^2 + \frac{x^2}{4})
Il ne reste plus qu'à multiplier par 4 et c'est bon.
L'idée est de réécrire l'expression sous la forme
avec
Je reconnais ici un polynôme (dans la parenthèse) de la forme
Or moi je veux arriver à
Il ne reste plus qu'à multiplier par 4 et c'est bon.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
