Polynome

[Tomjv]

Bonjour, j'ai des difficulté avec mon exercice, j'aimerai que l'on m'éclaire sur ce qu' est une racine d'un polynome



Merci de votre aide

[ampholyte]

Bonjour,

On te demande en question 1) de chercher sur internet la définition de racine d'un polynome ^^.

En mathématiques, une racine d'un polynôme P(X) est une valeur telle que P(;)) = 0. C'est donc une solution de l'équation polynomiale P(x) = 0, ou encore, un zéro de la fonction polynomiale associée. Par exemple, les racines de X2 – X sont 0 et 1.

Pour faire simple, soit x1 une racine du polynôme P(x) = ax² + bx + c (avec a, b et c réel), alors ax1² + bx1 + c = 0

Une racine est donc une valeur de x pour laquelle le polynôme s'annule.

[Tomjv]

Merci beaucoup, ta definition m' a mieux aidé :')

ducoup 3)
-5^3+6*-5^2+6*-5+5=0
-125+150-30+5=0
-125+125=0

[ampholyte]

C'est exactement cela, par contre il vaut mieux éviter le = 0 au début.

D(-5) = (-5)^3 + 6*(-5)^2 + 6*(-5) + 5
....
D(-5) = 0

Donc -5 est une racine de D(x).

[lulu math discovering]

En effet, il ne faut pas écrire le =0, sinon cela implique que tu sais déjà le résultat.

[Tomjv]

Ok merci beaucoup je le retiens )

[mathelot]

Soit P un polynome.

soit a un réel

Divisons P(x) par x-a
il vient

P(x)=(x-a)Q(x)+r

comme on a divisé par un diviseur de degré 1 (x-a), le reste est une constante r.

en remplaçant x par a

P(a)=r

P(x)=(x-a)Q(x)+P(a)

si P(a)=0 alors P est divisible par x-a
si P est divisible par x-a alors P(a)=0

[mathelot]

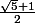
par exemple est racine de
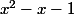
(faire le calcul)