Polynome du second degrès [1erS]

[Rogan]

Bonjour, J'aimerais un peus d'aide sur cette exercice :

Soit l'équation ax^2+bx+c=0 ; on suppose qu'elle admet 2 solutions u et v

1 . Exprimer en fonction de a, b et c les reels : u + v ; uv .

2 . en déduire simplement 1/u+1/v ; u^2+v^2 ; 1/u^2+1/v^2 .

Merci d'avance pour ceux qui m'aiderons.

[rene38]

Bonjour

Tu supposes que l'équation a 2 solutions et tu écris ces 2 solutions qui s'appellent u et v.
La suite consiste à
additionner ces 2 solutions pour obtenir u+v
multiplier ces 2 solutions pour obtenir uv
.............

[becirj]

Bonjour

1) Tu calcules u et v en utilisant les formules que tu as vu en claase.

2) Toutes les expressions à calculer peuvent s'exprimer en fonction de u et v et tu remplaces par ce que tu as trouvé à la première question.

[julian]

Bonjour,
Il faut que tu calcules ces 2 racines (on te dis que l'on suppose car ne connaissant pas a, b et c on ne pas pas forcément savoir).
Donc :



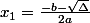
et
tu remplaces \Delta par b²-4ac