Ou alors quelque chose comme -0,5r^2-1/8r^2sqrt(16-pi^2)?
Si on peut enlever le divisé par 128?
Polynôme du Second Degré
28 messages
- Page 2 sur 2 - 1, 2
Re: Polynôme du Second Degré
Je devrai normalement le rendre demain, mais en re regardant au début j’ai eu une autre idée: est-il possible de mettre au tout départ -(pir^2)/4 dans le membre de gauche au lieu de multiplier par 4 pour enlever le divise par 4? Ne serait-ce pas plus facile?
Re: Polynôme du Second Degré
J’ai donc ensuite effectué le X1=x1^2, et tombe sur ça https://ibb.co/HXmcptX est ce correct?
Re: Polynôme du Second Degré
Bonjour,
64X² - 64R²*x - Pi²*R^4 = 0
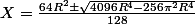
on divise numérateur et dénominateur par 16 (attention à la racine carrée ...)
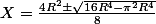
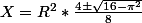
Et on se rappelle que X = x² -->
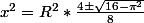
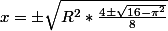
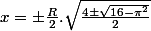
Mais attention, il faut savoir ce que représente x dans le problème ... il se pourrait bien que c'est une longueur, qui alors doit être positive.
Et si oui, alors il ne faut garder que les valeurs positives de x, soit :
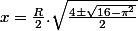
ou si on préfère :
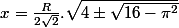

64X² - 64R²*x - Pi²*R^4 = 0
on divise numérateur et dénominateur par 16 (attention à la racine carrée ...)
Et on se rappelle que X = x² -->
Mais attention, il faut savoir ce que représente x dans le problème ... il se pourrait bien que c'est une longueur, qui alors doit être positive.
Et si oui, alors il ne faut garder que les valeurs positives de x, soit :
ou si on préfère :
28 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
