Polynôme non factorisable

[t.itou29]

Bonsoir,
Voici un petit problème

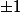
Soit p(x) un polynôme à coefficients dans Z de degré 1999 qui prend la valeur pour 1999 valeurs entières et différentes de x. Montrer que p n'est pas factorisable comme produit de polynôme à coefficients entiers.

J'aimerais bien avoir votre solution, j'en ai trouvé une mais j'ai l'impression qu'il en existe une très simple avec une astuce que je ne parviens pas à trouver...

Ps: j'ai considéré p(x)=a(x)b(x) et g(x)=a(x)+b(x) (et je suis même pas sûr que ce soit correct...)

[Ben314]

Salut,
On part de P=AB. Il y a donc 1999 valeurs différentes n t.q. A(n)B(n)=+-1 et donc A(n)=+-1 et B(n)=+-1.
Si A et B sont de degré respectif a et b alors a+b=1999 qui est impair donc un des deux, par exemple a est <1999/2 (strictement)
Le polynôme A²-1 est alors de degré 2a<1999 et il s'annule 1999 fois : il est donc identiquement nul donc A est constant (égal à 1 ou à -1)

[zygomatique]

Salut,
On part de P=AB. Il y a donc 1999 valeurs différentes n t.q. A(n)B(n)=+-1 et donc A(n)=+-1 et B(n)=+-1.
Si A et B sont de degré respectif a et b alors a+b=1999 qui est impair donc un des deux, par exemple a est <1999/2 (strictement)
Le polynôme A²-1 est alors de degré 2a<1999 et il s'annule 1999 fois : il est donc identiquement nul donc A est constant (égal à 1 ou à -1)

très joli ....

[t.itou29]

Salut,
On part de P=AB. Il y a donc 1999 valeurs différentes n t.q. A(n)B(n)=+-1 et donc A(n)=+-1 et B(n)=+-1.
Si A et B sont de degré respectif a et b alors a+b=1999 qui est impair donc un des deux, par exemple a est <1999/2 (strictement)
Le polynôme A²-1 est alors de degré 2a<1999 et il s'annule 1999 fois : il est donc identiquement nul donc A est constant (égal à 1 ou à -1)

Merci ! J'avais pensé à définir la fonction p^2-1 (dont on connait les 0 du coup) mais je n'arrivais pas à l'exploiter...
C'est vrai que c'est joli comme preuve !

[t.itou29]

J'ai un autre problème sur les polynômes :
Soit P un polynôme à coeffs dans Z, on suppose qu'il existe 4 entiers distincts a,b,c,d tels que P(a)=P(b)=P(c)=P(d)=5. Montrer qu'il n'existe pas d'entier k tel que P(k)=8.

Si on définit G par G(x)=P(x)-5 alors il existe un polynôme Q tel que:
G(x)=(x-a)(x-b)(x-c)(x-d)Q(x)
On cherche alors k tel que G(k)=3 or c'est impossible car chacun des 4 facteurs (x-a),..,(x-d) donne un entier différent dont le produit est donc différent de 3.

Est-ce correct ?

[zygomatique]

G(k) = (k - a)(k- b)(k - c)(k - d)Q(k) = 3 implique que k n'est a ni b ni c ni d donc k - a, k - b, k - c et k - d sont quatre diviseurs distincts de 3 .... qui n'en possède que 2

....

étonnant de prendre 4 entiers alors que 3 suffisent ...

[t.itou29]

G(k) = (k - a)(k- b)(k - c)(k - d)Q(k) = 3 implique que k n'est a ni b ni c ni d donc k - a, k - b, k - c et k - d sont quatre diviseurs distincts de 3 .... qui n'en possède que 2

....

Je savais bien c'était pas bien très rédigé :mur:
c'est plus clair comme ça ! Merci

[Ben314]

étonnant de prendre 4 entiers alors que 3 suffisent ...

Il me semble bien que non :
Si on avait uniquement G(k) = (k - a)(k- b)(k - c)Q(k) on pourrait parfaitement avoir k-a=1 ; k-b=-1 ; k-c=3 et Q(k)=1
par exemple : k=0 ; a=-1 ; b=1 ; c=-3 et Q(X)=1 donc P(X)=5+(X+1)(X-1)(X+3) qui vaut 5 en -3, 1 et 3 et qui vaut 8 en 0.

Et c'est effectivement "mal rédigé" vu que ce n'est pas 4 diviseurs distincts que l'on a mais seulement 3 : rien n'impose à G(k) d'être différent des 3 autres.

[zygomatique]

bien sur ... j'ai raisonné "dans les positifs" !!!

évidemment dans Z 3 possède quatre diviseurs distincts ...

:lol3:

[Ben314]

étonnant de prendre 4 entiers alors que 3 suffisent ...

Il me semble bien que non :
Si on avait uniquement G(k) = (k - a)(k- b)(k - c)Q(k) on pourrait parfaitement avoir k-a=1 ; k-b=-1 ; k-c=3 et Q(k)=1
par exemple : k=0 ; a=-1 ; b=1 ; c=-3 et Q(X)=1 donc P(X)=5+(X+1)(X-1)(X+3) qui vaut 5 en -3, 1 et 3 et qui vaut 8 en 0 (un nombre premier p ne possède que 2 diviseurs dans N, mais il en possède 4 dans Z...)

Et c'est effectivement "mal rédigé" vu que ce n'est pas 4 diviseurs distincts que l'on a mais seulement 3 : rien n'impose à G(k) d'être différent des 3 autres.

EDIT : grilled par... Zygomatique lui même...

[zygomatique]

étonnant je réponds à ton msg "avant" le tien ....

oui je ne fais aucune hypothèse sur Q(k) ....

oui mais avec quatre entiers on a 4 diviseurs distincts autre que Q(k)

il faut effectivement en prendre 4 ... et changer de rédaction ...

et alors on conclut que |G(k)| > 3 donc G(k) n'est pas 3 ....

[Ben314]

étonnant je réponds à ton msg "avant" le tien ....

Là, je me rapelle même plus si je l'ai fait ou pas, mais il m'arrive assez fréquemment de :
1) Taper une réponse en n'ayant pas super réfléchi et en n'ayant pas totalement lu les post précédents.
2) Me demander ensuite si je n'ai pas écrit une c... ou bien un truc déjà remarqué dans un des posts précédents.
3) Effacer le message après en avoir fait un "copier" (ctrl C).
4) Éventuellement réinser & modifier le message après avoir vérifier sa (relative... :zen:) pertinence.

[zygomatique]

Là, je me rapelle même plus si je l'ai fait ou pas, mais il m'arrive assez fréquemment de :
1) Taper une réponse en n'ayant pas super réfléchi et en n'ayant pas totalement lu les post précédents.
2) Me demander ensuite si je n'ai pas écrit une c... ou bien un truc déjà remarqué dans un des posts précédents.
3) Effacer le message après en avoir fait un "copier" (ctrl C).
4) Éventuellement réinser & modifier le message après avoir vérifier sa (relative... :zen:) pertinence.

il faut dire que nos deux msg ont été édité à la même heure mais le mien était une réponse au tien (que j'ai pris pourtant le temps de lire et réfléchir) dont j'ai été étonné qu'il apparaisse avant le tien car il a du s'écouler tout de même un certain temps ... comme aurait dit Fernand Raynaud ....

c'est pourquoi mon autocorrection est en fait de ton fait !!!!

:lol3:

[Ben314]

@t.itou29 : si tu cherche un exo un peu du même style sur les polynômes, il y a celui là (tiré de je sais plus quelle olympiades ou autre...) :
Soit P un polynôme à coeff. réels de degré <=2014 tel que, pour tout entier , on ait
Quelle est la valeur de P(2015) ?

[t.itou29]

@t.itou29 : si tu cherche un exo un peu du même style sur les polynômes, il y a celui là (tiré de je sais plus quelle olympiades ou autre...) :
Soit P un polynôme à coeff. réels de degré <=2014 tel que, pour tout entier , on ait
Quelle est la valeur de P(2015) ?

Justement c'était un exemple dans mon cours (c'est l'USAMO 1975) et comme la solution était sur la même page (quelle idée !) j'ai pas pu m'empêcher de regarder....