Bonjour,
Après avoir tracé C,une parabole de P(x)=-x²-2x+3 avec P(x)=0, tracer la droite d d'équation y=2x-3.
D) déterminer graphiquement des valeurs approchées des abscisses des points d'intersection C et d.
Je trouve -5,2 et 1,2.
E) En quoi la question D permet-elle d'obtenir graphiquement les solutions de l'équation P(x)=0 ?
Et là... Je ne comprends même pas la question !
Merci d'avance pour vos éclaircissements.
Polynôme, intersection de droite et de parabole
8 messages
- Page 1 sur 1
Re: Polynôme, intersection de droite et de parabole
bonjour
je ne trouve pas ça et en plus je trouve deux points d'intersections
on est d'accord on a bien=-x^2-2x+3) et
et 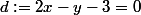
je ne trouve pas ça et en plus je trouve deux points d'intersections
on est d'accord on a bien
Re: Polynôme, intersection de droite et de parabole
Bonjour et merci pour ce retour rapide.
On a P(x)=-x²-2x+3 qu'il faut tracer pour P(x)=0 et la droite d d'équation y=2x-3.
En utilisant un traceur de courbe online, je trouve les mêmes courbes que sur mon papier.
Oui je trouve 2 points d'intersection, comme indiqué dans mon post initial le premier d'abscisse -5,2 et le second d'abscisse 1,2.
On a P(x)=-x²-2x+3 qu'il faut tracer pour P(x)=0 et la droite d d'équation y=2x-3.
En utilisant un traceur de courbe online, je trouve les mêmes courbes que sur mon papier.
Oui je trouve 2 points d'intersection, comme indiqué dans mon post initial le premier d'abscisse -5,2 et le second d'abscisse 1,2.
Re: Polynôme, intersection de droite et de parabole
réponse de correction :
ah oui pardon j'ai lu rapidement sans faire attention
effectivement
ah oui pardon j'ai lu rapidement sans faire attention
effectivement
Re: Polynôme, intersection de droite et de parabole
quelques précisions:
L'équation P(x)=0 revient à l'équation:
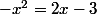
les solutions de l'équation sont donc les abscisses des points d'intersection de la droite (d)
d'équation y=2x-3 et de la parabole (M) d'équation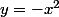
L'équation P(x)=0 est équivalente à
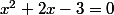
(x+3)=0)
les racines sont donc 1 et -3
L'équation P(x)=0 revient à l'équation:
les solutions de l'équation sont donc les abscisses des points d'intersection de la droite (d)
d'équation y=2x-3 et de la parabole (M) d'équation
L'équation P(x)=0 est équivalente à
les racines sont donc 1 et -3
Re: Polynôme, intersection de droite et de parabole
les solutions de l'équation sont donc les abscisses des points d'intersection de la droite (d)
d'équation y=2x-3 et de la parabole (M) d'équation y = - x²
@mathelot
(je m'immisce dans l'exo)
la parabole que l'énoncé demande de tracer est celle d'équation y = -x²-2x+3
et pas y = - x²
comme Hexa je ne comprends pas la question
Re: Polynôme, intersection de droite et de parabole
Moi je pense comme mathelot, que le but de l'exo est de ramener un problème d'intersection de la parabole 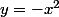 avec la droite
avec la droite 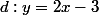 au problème d'intersection d'une nouvelle parabole
au problème d'intersection d'une nouvelle parabole 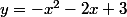 avec l'axe des abscisses.
avec l'axe des abscisses.
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 89 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
