Polynôme du 3ème degré

[marce-eux]

Salut à tous !
J'ai un question dans un exercice que je n'arrive pas à résoudre

Voilà la question :
Déterminer un polynôme Q du troisième degré tel que l'on ait, pour tout réel x

Q(x+1)-Q(x)=x²

Merci pour vos réponses

[Ericovitchi]

Pourquoi ne pas le chercher sous sa forme ax³ +bx²+cx+d ?
tu formes Q(x+1)-Q(x) et tu identifies chaque terme avec x²
ça te fera un système en a,b,c,d

[Olympus]

Salut !

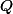
Comme est un polynôme du troisième degré, il existe des réels tels que . On peut d'ailleurs remarquer vite fait que d'après l'équation, peut valoir tout et n'importe quoi .

On a


Or deux polynômes sont égaux si et seulement si leurs coefficients le sont, donc ...