Points commun d'une droite paramétrée

[anna27]

Soit : Dp : (1-p²)x+2py+(p²-2p-3)=0
Existe t il un pt qui soit commun à toutes les Dp

Comment faut il procéder ?

[Ben314]

Salut,
Il y a plusieurs méthodes :
1) Tu regarde ton équation comme ayant comme seule variable p (donc x et y sont des paramètres supposés constants) et tu regarde à quelle condition cette équation est vraie pour tout réel p.
2) Tu cherche l'intersection de deux droites, par exemple D0 et D1 et tu regarde si le(s) point(s) d'intersection trouvé(s) sont sur toutes les autres droites.

[anna27]

J'ai essayé la 2ème méthode car la première je ne la comprend pas

D0 : x=3
D1 y=2

Donc le pt d'intersection est (3,2)

Et si on vérifie si ce pt appartient à toutes les droites, je remplace ces coordonnées dans Dp :
2p(1-p)=0 on trouve p=0 ou p=1 pour que ce point appartient donc pas quelque soit p...
mais je ne vois pas comment conclure

[Ben314]

Ben tu conclue par du "blabla" pour expliquer précisément ce que tu as fait :

S'il existe un point appartenant à toutes les droites Dp, alors, bien entendu, il doit appartenir à la fois à D0 et à D1.
Or le seul point appartenant à la fois à D0 et D1 est le point (3,2) :
C'est donc le seul point qui peut, éventuellement, appartenir à toutes les droites Dp.
Or il n'appartient pas à D2 donc il n'appartient pas à toutes les droites Dp.

FIN

(en fait tu as même montré que le point (2,3) n'appartient qu'aux seules droites D0 et D1 et à aucune autre, mais de dire qu'il n'appartient pas à D2, ça suffit pour montrer qu'il n'y a aucun points sur toutes les droites en même temps)

[Ben314]

Sinon, la méthode 1, ça consistait à dire que peut s'écrire qui est de la forme .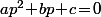

Or, pour que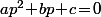 pour tout réel , il faut que .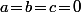
Sauf qu'ici, on a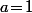 , donc, quelque soient les valeurs de et de , on ne pourra jamais avoir pour tout réel .

[anna27]

Grand merci