[Complexes] Point appartenant à un arc

par **Olympus** » 21 Juin 2010, 21:12

Bonsoir !

J'essaie de me mettre un petit peu à la géométrie avec les complexes, et je tombe sur la propriété suivante :

En considérant AB un arc du cercle unité, si C appartient à cet arc, alors :

Mais comme ça fait juste quelque temps que j'ai attaqué les complexes, je bloque un peu à la démonstration de cette propriété ...

Pourriez-vous m'aider s'il vous plaît ?

Merci !

EDIT : Une corde pas un arc, toutes mes excuses

par **benekire2** » 21 Juin 2010, 21:19

Salut !

A quelle condition trois points sont cocycliques ?

PS: Cette propriété figure dans le titu ?

par **Ben314** » 21 Juin 2010, 21:22

Salut,
Je pense que ça va être dur à montrer vu que... c'est faux.
Par exemple, si a=1 et b=-1 (qui sont bien sur le cercle unité) l'égalité

dit que

ce qui signifie que

est sur l'axe des x...

P.S. : tu ne confondrait pas l'arc et la corde par hasard ?

par **benekire2** » 21 Juin 2010, 21:24

Salut ,

j'ai pas beaucoup d'idées pour démontrer ça mais ça doit pas être bien méchant. Essaye de voir avec a=e^ia et b=e^ib

il suffit de montrer que le module de c vaut 1. En triturant avec les angles moitiés ça doit se faire. Dis moi quand tu trouve.

PS: Tu l'as trouvé dans le titu celle ci ?

Edit: Grillé par ben et la preuve de l'impossibilité de la formule :hum:

par **Ben314** » 21 Juin 2010, 21:28

Effectivement : pour a et b fixé sur le cercle trigo, l'ensemble des c du plan complexe tels que

est la droite (ab) tout entière (dont la corde [ab] n'est quun petit morceaux).

C'est trés simple à voir : si on écrit

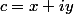
on voit (sans calculs) que l'équation de départ correspond à un système d'équations linéaires en

et

donc l'ensemble de solutions est vide OU c'est un point OU c'est une droite.
Sauf qu'il est clair que

et

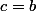
sont des solutions donc...

par **Olympus** » 21 Juin 2010, 21:52

Oula j'ai pas bien lu, c'était effectivement une corde et pas un arc, méa culpa :D

par **Olympus** » 21 Juin 2010, 22:53

Donc l'énoncé dit juste que si C appartient à la corde AB, alors il appartient à la droite passant par A et B, dont l'équation est justement

, rien de bien méchant en effet .

Pour benekire2 : euh nope, j'ai juste été curieux et j'ai regardé les propriétés listées ici ( article orienté IMO, comme d'habitude

) : http://www.imomath.com/tekstkut/cnum_mr.pdf .

par **Ben314** » 22 Juin 2010, 07:25

Attention : le Théorème 3 est "légèrement" faux : la quantité dont il parle s'appelle le birapport de a,b,c,d (c'est une notion naturelle dans la droite projective complexe) et, pour 4 points 2 à 2 distincts, le biraport est réel ssi les 4 points sont cocycliques (i.e. sur un même cercle) OU BIEN alignés (cela vient du fait que dans la droite projective complexe, les droites sont des cercles particuliers)

par **benekire2** » 22 Juin 2010, 08:30

Merci olympus :zen:

par **Olympus** » 22 Juin 2010, 10:45

Ben314 a écrit:Attention : le Théorème 3 est "légèrement" faux : la quantité dont il parle s'appelle le birapport de a,b,c,d (c'est une notion naturelle dans la droite projective complexe) et, pour 4 points 2 à 2 distincts, le biraport est réel ssi les 4 points sont cocycliques (i.e. sur un même cercle) OU BIEN alignés (cela vient du fait que dans la droite projective complexe, les droites sont des cercles particuliers)

Ah oki, merci pour la précision :we:

[Complexes] Point appartenant à un arc

[Complexes] Point appartenant à un arc

Qui est en ligne