Hum... je n'y arrive pas trop j'arrive a un truc plus compliqué qu'au départ donc ?!
:briques:
Le plus grand cornet ?
34 messages
- Page 2 sur 2 - 1, 2
par haricot29 » 14 Jan 2007, 10:17
je pars de :
V'(h) = 1/3pi ( 2r*rac(R²-r²) + r²* (-r/rac(R²-r²))
je mets toute la parenthese sur rac(R²-r²)
V'(h) = 1/3 pi (2r*(R+r) + (-r^3))
V'(h) = 1/3 pi * (2Rr+2r²-r^3)
V'(h) = 1/3 pi * r*(2R+2r-r²)
là c'est simplifier mais je fais quoi apres j'isole r ? c'est ok comme simplification ?
V'(h) = 1/3pi ( 2r*rac(R²-r²) + r²* (-r/rac(R²-r²))
je mets toute la parenthese sur rac(R²-r²)
V'(h) = 1/3 pi (2r*(R+r) + (-r^3))
V'(h) = 1/3 pi * (2Rr+2r²-r^3)
V'(h) = 1/3 pi * r*(2R+2r-r²)
là c'est simplifier mais je fais quoi apres j'isole r ? c'est ok comme simplification ?
par Quidam » 14 Jan 2007, 11:23
haricot29 a écrit:il a quelq'un ?
Oui, une seconde, je viens de me réveiller... Je réponds !
par Quidam » 14 Jan 2007, 11:40
Il y a des erreurs de calcul !
Ca c'est bon !
C'est ce qu'il fallait faire, mais là, tu t'es trompée ! Il fallait écrire :
 = \frac{1}{3}\pi\frac{2r(R^2-r^2)-r^3}{\sqrt{R^2-r^2})
 = \frac{1}{3}\pi\frac{2rR^2-2r^3-r^3}{\sqrt{R^2-r^2})
 = \frac{1}{3}\pi\frac{2rR^2-3r^3}{\sqrt{R^2-r^2})
 = \frac{1}{3}\pi\frac{r(2R^2-3r^2)}{\sqrt{R^2-r^2})
La dérivée s'annulle pourR)
Sauf erreur...
haricot29 a écrit:
Ca c'est bon !
haricot29 a écrit:je mets toute la parenthese sur rac(R²-r²)
C'est ce qu'il fallait faire, mais là, tu t'es trompée ! Il fallait écrire :
La dérivée s'annulle pour
Sauf erreur...
par haricot29 » 14 Jan 2007, 11:51
a ok d'accord je vois, oui c'est ok j'ai vérifier a la calculatrice pas d'erreur Lool
pour trouver le h pour que V(h) soit maximal je fais comment je remplace r par rac(2/3)R dans V(h) ?! :hein:
pour trouver le h pour que V(h) soit maximal je fais comment je remplace r par rac(2/3)R dans V(h) ?! :hein:
par haricot29 » 14 Jan 2007, 16:03
si il y a quelqu'un se serait cool car c'est pour demain donc il me reste plus trop de temps ! Merci d'avance :++:
par haricot29 » 14 Jan 2007, 18:49
si il y a quelqu'un se serait cool car c'est pour demain donc il me reste plus trop de temps ! SVP... ça fait presque 10jours que je suis dessus se serait dommage ! Merci d'avance
par haricot29 » 14 Jan 2007, 19:55
ok donc je dis juste que pour que v(h) soit max il suffit que h = rac(R²-(rac(2/3)R)²) ?! C'est ça ?
par haricot29 » 14 Jan 2007, 19:59
et puis pour calculer alpha je travail ac :
V(h) = 1/3*pi*[(2pi-alpha)/(2pi)]*R*rac(R²-r²)
et j'isole alpha et je trouveré la réponse ?!
C'est ça ?!
C'es parce que j'ai a tout pris envie de finir cet exo c'est pour cela !Merci d'avance :id: :id:
V(h) = 1/3*pi*[(2pi-alpha)/(2pi)]*R*rac(R²-r²)
et j'isole alpha et je trouveré la réponse ?!
C'est ça ?!
C'es parce que j'ai a tout pris envie de finir cet exo c'est pour cela !Merci d'avance :id: :id:
par Quidam » 14 Jan 2007, 20:47
haricot29 a écrit:ok donc je dis juste que pour que v(h) soit max il suffit que h = rac(R²-(rac(2/3)R)²) ?! C'est ça ?
Oui, mais sache que :
par Quidam » 14 Jan 2007, 20:48
haricot29 a écrit:et puis pour calculer alpha je travail ac :
V(h) = 1/3*pi*[(2pi-alpha)/(2pi)]*R*rac(R²-r²)
et j'isole alpha et je trouveré la réponse ?!
C'est ça ?!
C'es parce que j'ai a tout pris envie de finir cet exo c'est pour cela !Merci d'avance :id: :id:
Avec r et R, tu trouves
34 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
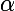
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :