Plan complexe et suites
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 16:31
par Elda Saphira » 15 Déc 2010, 16:31
[LEFT]
Énoncé :
Soit rn = r0*q^n = r0*(2/3)^n
et  n =
n =  0+2;)/3*n (avec
0+2;)/3*n (avec  = pi)
= pi)
Pour chaque entier naturel n, on pose zn=rn(cos;)n+isin;)n). Sachant que z0, z1, z2 sont liés por la relation z0z1z2=8, déterminer le module et un argument de z0, z1, z2.
Là j'ai trouvé :
 z0;)= 3
z0;)= 3  z1;)= 2 et
z1;)= 2 et  z2;)= 4/3
z2;)= 4/3
et  0 = 2;)/3
0 = 2;)/3  1 = 4;)/3 et
1 = 4;)/3 et  2 = 2;)
2 = 2;)Dans le plan complexe P muni d'un repère orthonormé direct (O,u,v), on appelle Mn le point d'affixe zn.
a) pour tout entier naturel n, calculer

vecteur :MnMn+1;) en fonction de n.
b) On pose ln=;)(n k=0)

vecteur : MkMk+1;). Calculer ln en fonction de n et déterminer la limite de ln quand n tend vers +;)[/LEFT]
Là j'ai penser à une récurrence mais je vois pas comment faire
Merci pour votre aide
-
Sylviel
- Membre Transcendant
- Messages: 6466
- Enregistré le: 20 Jan 2010, 12:00
-
 par Sylviel » 15 Déc 2010, 16:41
par Sylviel » 15 Déc 2010, 16:41
Commence déjà par exprimer la longueur que tu cherche à mesurer (pour n fixé). Je ne penses pas que la reccurence soit d'une utilité quelconque, mais sait-on jamais ?
Donc que vaut ||MnMn+1||? (commence par le donner en fonction de zn et zn+1)
Merci de répondre aux questions posées, ce sont des indications pour vous aider à résoudre vos exercices.
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 17:04
par Elda Saphira » 15 Déc 2010, 17:04
On obtient : ||Zn+Zn+1||=|| rn(cos;)n+isin;)n) + rn+1 (cos(;)n+1)+isin(;)n+1)) ||
= || rn(cos;)n+isin;)n) + rn*2/3 [cos(;)n+2;)/3)+isin(;)n+2;)/3)] ||
= || rn[cos(;)0+2;)/3*n)+isin(;)0+2;)/3*n)] + rn*2/3 [cos(;)n+2;)/3)+isin(;)n+2;)/3)] ||
=||rn[cos(;)0+2;)/3*n)+isin(;)0+2;)/3*n)] + rn*2/3 [cos(;)0+2;)/3*n+2;)/3)+isin(;)0+2;)/3*n+2;)/3)]||
=||r0*2/3^n[cos(;)0+2;)/3*n)+isin(;)0+2;)/3*n)] + r0*2/3^n+1 [cos(;)0+2;)/3*n+2;)/3)+isin(;)0+2;)/3*n+2;)/3)]||
C'est ça qu'il faut faire ?!?!? :help:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 17:15
par Arnaud-29-31 » 15 Déc 2010, 17:15
Bonjour,
As-tu vu l'exponentielle complexe ? C'est bien plus simple pour isoler module et argument.
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 17:24
par Elda Saphira » 15 Déc 2010, 17:24
Oui j'ai vu l'écriture exponentielle des nombres complexes
Ici ça donne :
||MnMn+1|| = || [rn+1*exp(;)n+1)] - [rn*exp(;)n)] ||
= || [rn*2/3*exp(;)n+2;)/3)] - [rn*exp(;)n)] ||
C'est ça ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 17:27
par Arnaud-29-31 » 15 Déc 2010, 17:27
Oui c'est un bon début. (Sans oublier le i dans l'exponentielle bien sûr ^^)
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 17:37
par Elda Saphira » 15 Déc 2010, 17:37
Donc :
||MnMn+1|| = || [rn+1*exp(i;)n+1)] - [rn*exp(i;)n)] ||
= || [rn*2/3*exp(i;)n+2;)/3)] - [rn*exp(i;)n)] ||
On peut dire que c'est égale à || -1/3*rn*exp(2;)/3) || ou c'est une énormité ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 17:50
par Arnaud-29-31 » 15 Déc 2010, 17:50
Je vais te laisser répondre à cette question ...
Si tu arrives à joindre la première et la dernière ligne par des calculs et transformations qui tiennent la route, alors il y a des chance pour que la dernière ligne soit juste. Sinon il y a des chances pour que ce soit faux ...
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 17:53
par Elda Saphira » 15 Déc 2010, 17:53
Merci pour ton aide :lol4:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 17:54
par Arnaud-29-31 » 15 Déc 2010, 17:54
Bon ... évidemment c'est faux.
Tu viens d'écrire que
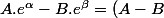.e^{\alpha - \beta})
... c'est clairement une "énormité".
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 18:11
par Elda Saphira » 15 Déc 2010, 18:11
C'est bien que je pensais
*honte à moi ! ^^*
J'en suis à :
|| 2/3*rn*exp(i;)n+2;)/3) - rn*exp(i;)n) ||
= || rn*[2/3*exp(i;)n +2;)/3) - exp(i;)n)] ||
= || rn*[2/3*exp(i;)n)*(-3/2 + exp(2;)/3) )]
= || (2/3)^n*[2*exp(i;)n)*(-3/2 + exp(2;)/3) ] ||
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 18:13
par Arnaud-29-31 » 15 Déc 2010, 18:13
Oui, on peut factoriser par
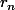
, maintenant il faudrait casser le
})
-
Elda Saphira
- Membre Naturel
- Messages: 24
- Enregistré le: 24 Oct 2010, 17:49
-
 par Elda Saphira » 15 Déc 2010, 18:28
par Elda Saphira » 15 Déc 2010, 18:28
|| rn*[2/3*exp(i;)n +2;)/3) - exp(i;)n)] ||
= || rn*[2/3*exp(i;)n)*(-3/2 + exp(2;)/3) )]
= || (2/3)^n*[2*exp(i;)n)*(-3/2 + exp(2;)/3) ] ||
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 15 Déc 2010, 18:56
par Arnaud-29-31 » 15 Déc 2010, 18:56
Je ne comprends pas ce que tu as fait là ... on est d'accord que

?
Le i dans l'exponentielle est aussi facteur de
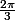
, fais attention aux parenthèses.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 108 invités
