Peu etre Une Petite Erreur D'énoncé

[mathmath06]

Donc Voila Mon enoncé me donne dans un plan Orthonormal les points A(-1;0) B(2;V3), C(2;-V3) et D(3;0)
(Ps:V c'est la racine Carrée Je la trouve pas sur mon clavier :stupid: )
La question etant de montrer que D est le barycentre des points Pondérés {(A;-1) ;(B;2) ;(C;2) } apres Quelques essaies je n'arrive pa a trouver que -DA+2DB+2DC=0 es-ce moi ou y a t-il une erreur d'enoncé ? Image du repere

[bombastus]

Bonjour!

Je ne vois pas d'erreur dans l'énoncé,
qu'as-tu essayé de faire?

[mathmath06]

J'ai Fait : - DA +2 DB +2 DC doit etre egale au vecteur 0
AD+2DB+2DC=4+2*2+(-2*2)=4 :briques:

[bombastus]

Je ne comprends pas comment tu trouves :
AD+2DB+2DC=4+2*2+(-2*2)=4
Que représente ce calcul? dans ton exemple, AD, DB, et DC sont des longueurs? des vecteurs?

[Black Jack]

Tu confonds longueur et vecteur, ce que tu dois montrer est:



:zen:

[mathmath06]

exact j'ai confondu les vecteurs mais a la sortie je trouve que : tous est en vecteur bien sur :marteau:

-DA+2DB+2DC=AD+2DA+2AB+2DA+2AC

Or B et C sont Symetrique par rapport a l axe des abscisses car ils possedent le meme abscisse mais leurs ordonnés sont opposé donc AB=-AC

donc

AD+2DA-2AC+2DA+2AC=3DA ...

Ou est cette erreur qui me tue depuis 2 jours ... :cry:

[rene38]

Bonsoir

Or B et C sont symétriques par rapport à l'axe des abscisses car ils possèdent la même abscisse mais leurs ordonnées sont opposées donc AB=-AC

Certes non ! (fais un dessin)
Commence par calculer les coordonnées des différents vecteurs.

[mathmath06]

c'est ce que je vien de fair mais je ne vois pas par ou passer :hum:

[Geek-R]

J'vois pas l'image du repère. Heberge la sur :

http://www.imageshack.us

Et pour les racines carrés, c'est :

[bombastus]

Maintenant que tu as les coordonnées des vecteurs, tu utilises le fait que :
-

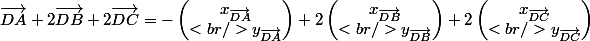
[Clembou]

J'vois pas l'image du repère. Heberge la sur :

http://www.imageshack.us

Et pour les racines carrés, c'est :

Ou en LaTeX : \sqrt... Cela donne par exemple

PS : Il est conseillé d'utiliser le LaTeX sur le forum pour avoir une présentation plus claire de l'énoncé. :id:

[bombastus]

Maintenant que tu as les coordonnées des vecteurs, tu utilises le fait que :
-
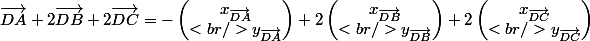
Donc il suffit de montrer que :

[Black Jack]

rappels théoriques :

a)
Si on a les points A(x1 ; y1) et B(x2 ; y2) et C(x3 ; Y3) et D(x4 ; Y4)
Les coordonnées du vecteur AB sont(x2-x1 ; y2-y1)
Les coordonnées du vecteur CD sont(x4-x3 ; y4-y3)

Si P et Q sont 2 réels,
Les coordonnées du vecteur sont (P(x2-x1) + Q(x4-x3) ; P(y2-y1) + Q(y4-y3))

b)
Un vecteur est le vecteur nul si ses 2 coordonnées sont nulles.

Si tu comprends ce qui est écrit ci-dessus, tu dois arriver à résoudre ton exercice.

:zen:

[mathmath06]

Voila le repere

[mathmath06]

oui j'ai bien compris merci bien :D

[mathmath06]

Une Petite question On Me dit que E ensemble des points M du plan tels que

(-MA+2MB+2MC).CD=12 tout est en vecteur bien sur (je suis entrain de me mettre a latex pour bientot c jurer ;) apres avoir montrer que

(-MA+2MB+2MC).CD=12 equivaut a DM.CD=-4

On demande de verifier que le point A appartient a E
Par quel moyen on peut le prouver ?

[bombastus]

E est l'ensemble des points M du plan tels que
(-MA+2MB+2MC).CD=1 ( équivalent à DM.CD=-4)

On te demande de montrer que A appartient à E, c'est à dire que A vérifie la même propriété que les points M de E.

[mathmath06]

C'est okay j'ai bien compris et j'ai tout prouver :id:
Apres la derniere question Je vois pas comment faire parce avant on ma demander de montrer que DM.CD=-4=> AM.DC=0 (en vecteur) ce qui facile a demontrer il faut ensuite en deduire l'ensemble E es-ce que je dis puisque que A appartient a E or AD=4 (longueur)on peut dire que Tout point M verifiant que DM=4 (longueur) appartient a E ?

[bombastus]

Pourquoi le fait que AD=4 entraînerai que DM=4?
Tu dois juste utiliser : , quel est l'ensemble des points M qui vérifient cette relation?

[mathmath06]

Sous quel forme je dois le trouver ?