Un peu d'aide SVP :) (vecteurs)
19 messages
- Page 1 sur 1
Un peu d'aide SVP :) (vecteurs)
Bonjour, je galère actuellement avec le problème de maths suivant concernant les vecteurs :
On considère un triangle ABC avec AB=5 cm et AC=9 cm
1.Construire le point C' tel que CC'(vecteur)=4/5BA(vecteur).
2.Soit B' le point tel que 4B'A(vecteur)+5B'C(vecteur)=0(vecteur).
3.Exprimer le vecteur BB' en fonction des vecteurs AB et AC.
4.Même question pour le vecteur BC'.
5.Que peut-on déduire pour les points B,B'et C'?
6.Par C', on trace la parallèle à (BC); elle coupe (AB) en A'.
**a)Montrer que AA'(vecteur) et CC'(vecteur) sont colinéairesen calculant le réel ktel que AA'=kCC'.
**b)Exprimer A'B'(vecteur) puis AC'(vecteur) en fonction de AB(vecteur) et AC(vecteur).
**c)Les droites (A'B') et (AC')sont-elles parallèles?
Merci d'avance.
On considère un triangle ABC avec AB=5 cm et AC=9 cm
1.Construire le point C' tel que CC'(vecteur)=4/5BA(vecteur).
2.Soit B' le point tel que 4B'A(vecteur)+5B'C(vecteur)=0(vecteur).
3.Exprimer le vecteur BB' en fonction des vecteurs AB et AC.
4.Même question pour le vecteur BC'.
5.Que peut-on déduire pour les points B,B'et C'?
6.Par C', on trace la parallèle à (BC); elle coupe (AB) en A'.
**a)Montrer que AA'(vecteur) et CC'(vecteur) sont colinéairesen calculant le réel ktel que AA'=kCC'.
**b)Exprimer A'B'(vecteur) puis AC'(vecteur) en fonction de AB(vecteur) et AC(vecteur).
**c)Les droites (A'B') et (AC')sont-elles parallèles?
Merci d'avance.
Bonsoir,
Si tu as fait les questions 5) et 6.a), c'est que tu as su placer les points C' et B'.
Dans ce cas, je ne comprends pas en quoi on peut t'aider pour les questions 1), 2).
Tu as dû faire un dessein ou un shéma ? Quels sont tes résultats ? Ou sont les points C' et B' ?
J'imagine qu'il n'y a que les questions 3) et 4) qui posent problème ?
Si tu as fait les questions 5) et 6.a), c'est que tu as su placer les points C' et B'.
Dans ce cas, je ne comprends pas en quoi on peut t'aider pour les questions 1), 2).
Tu as dû faire un dessein ou un shéma ? Quels sont tes résultats ? Ou sont les points C' et B' ?
J'imagine qu'il n'y a que les questions 3) et 4) qui posent problème ?
Oui, c'est bien cela.
Le point B' est sur le segment AC à 5 cm de A et 4 cm de C.
Remarque que la notion de droite ou de gauche n'a pas de sens. Comme la position des points C' et B' est définie à partir de vecteurs, il suffit de déplacer B ou C pour que la figure se transforme. Et donc à droite ou à gauche n'a de sens que si l'on considère la figure de mon post précèdent.
Car, la figue ci-dessous est elle aussi correcte, mais le point B' apparait à gauche de A !

Il nous est demandé d'exprimer le vecteur en fonction des vecteurs
en fonction des vecteurs  et
et  .
.
(Sous entendu, uniquemetn à partir de ces deux vecteur).
As-tu avancé dans cette question ?
Le point B' est sur le segment AC à 5 cm de A et 4 cm de C.
Remarque que la notion de droite ou de gauche n'a pas de sens. Comme la position des points C' et B' est définie à partir de vecteurs, il suffit de déplacer B ou C pour que la figure se transforme. Et donc à droite ou à gauche n'a de sens que si l'on considère la figure de mon post précèdent.
Car, la figue ci-dessous est elle aussi correcte, mais le point B' apparait à gauche de A !

Il nous est demandé d'exprimer le vecteur
(Sous entendu, uniquemetn à partir de ces deux vecteur).
As-tu avancé dans cette question ?
OK.
Alors, comme on a aps d'indice, le mieux est de commencer par décomposer logiquement.
On considère B'B et on essaye de le décomposer à partir des vecteurs et points que l'on a sur la figure.
En général, une décomposition consiste à partir du premier point du vecteur, de faire un tour et de revenir au second point.

ici c'est simple je pars de B' vers A puis de A vers B.

Tiens, j'ai déjà dans mon expression le vecteur
Voyons si l'on peut faire apparaitre le vecteur à partir de
à partir de 
As-t-tu une idée ? Sachant que l'on a montré à la question 2) que B' est sur le segment (AC) et à 5 cm de A !
Alors, comme on a aps d'indice, le mieux est de commencer par décomposer logiquement.
On considère B'B et on essaye de le décomposer à partir des vecteurs et points que l'on a sur la figure.
En général, une décomposition consiste à partir du premier point du vecteur, de faire un tour et de revenir au second point.

ici c'est simple je pars de B' vers A puis de A vers B.
Tiens, j'ai déjà dans mon expression le vecteur
Voyons si l'on peut faire apparaitre le vecteur
As-t-tu une idée ? Sachant que l'on a montré à la question 2) que B' est sur le segment (AC) et à 5 cm de A !
Pourtant, le moyen utilise les mêmes notions que celle qui t'ont permis de placer B' sur la droite (AC).
Comment as-tu déterminé que B' est sur la droite (AC) et sur le segment [AC] à 5 cm de A ?
Par aileurs, si l'on considère les vecteurs et
et 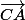 comment peut-on les qualifier l'un par rapport à l'autre ? (C'est à dire comment sont-ils l'un par rapport à l'autre ?).
comment peut-on les qualifier l'un par rapport à l'autre ? (C'est à dire comment sont-ils l'un par rapport à l'autre ?).
Comment as-tu déterminé que B' est sur la droite (AC) et sur le segment [AC] à 5 cm de A ?
Par aileurs, si l'on considère les vecteurs
Oui, c'est à peu près cela.
Mais c'est plus clair si l'on remet les choses dans l'ordre.
On sait que B' est placé de façon à ce que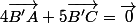
On peut donc écrire :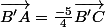
Ce qui prouve que les vecteurs et
et  sont colinéaires.
sont colinéaires.
(C'est ça la notion que j'attendais, et c'est d'ailleurs la notion de base de cet excercice.)
Donc et
et  sont colinéaires, mais de sens opposés.
sont colinéaires, mais de sens opposés.
Deux vecteurs colinéaires ont même direction.
Hors et
et  ont tous les deux comme origine le point B'.
ont tous les deux comme origine le point B'.
Comme ils sont colinéaires, cela signifie qu'ils sont porté par la même droite. En l'occurance la droite (AC).
En conséquence, le point B' est un point de la droite (AC).
Pour savoir où se situe le point B' sur cette droite (AC), on considère comme tu l'as très bien fait les amplitudes (normes est peut-être le terme plus adapté ici):
Comme, les deux vecteurs sont colinéaires à la droite (AC), on peut par projection sur celle-ci déduire que :
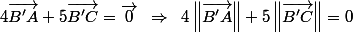 soit algébraiquement sur lad roite (AC) :
soit algébraiquement sur lad roite (AC) : 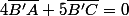 soit
soit 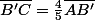
Par ailleurs, comme B' appartient à la droite (AC), on déduit donc par décomposition et projection sur cette même droite :
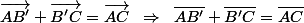
De ces deux équation algébriques, on en déduit que B' est sur sur le segment [AC] à une distance AB'=5 cm du point A.
Pour la réponse 3), on utilise les mêmes expressions pour obtenir l'expression de \vec{AB'} en fonction de \vec{AC}:
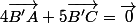
=\vec{0})
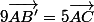
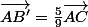
D'où,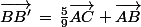

Pour la question 4), ce nest pas plus compliqué.
On commence par décomposer le vecteur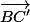 de la même façon, on part du point B et on parcours les vecteurs connus de façon à arriver au point final C'.
de la même façon, on part du point B et on parcours les vecteurs connus de façon à arriver au point final C'.
Jai marqué les vecteurs sur la figure ci-dessus.
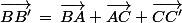
Tiens, bonne surprise, il y a déjà dans cette expression les vecteurs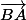 et
et  .
.
A toi de continuer en cherchant à faire disparaitre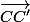 .
.
Mais c'est plus clair si l'on remet les choses dans l'ordre.
On sait que B' est placé de façon à ce que
On peut donc écrire :
Ce qui prouve que les vecteurs
(C'est ça la notion que j'attendais, et c'est d'ailleurs la notion de base de cet excercice.)
Donc
Deux vecteurs colinéaires ont même direction.
Hors
Comme ils sont colinéaires, cela signifie qu'ils sont porté par la même droite. En l'occurance la droite (AC).
En conséquence, le point B' est un point de la droite (AC).
Pour savoir où se situe le point B' sur cette droite (AC), on considère comme tu l'as très bien fait les amplitudes (normes est peut-être le terme plus adapté ici):
Comme, les deux vecteurs sont colinéaires à la droite (AC), on peut par projection sur celle-ci déduire que :
Par ailleurs, comme B' appartient à la droite (AC), on déduit donc par décomposition et projection sur cette même droite :
De ces deux équation algébriques, on en déduit que B' est sur sur le segment [AC] à une distance AB'=5 cm du point A.
Pour la réponse 3), on utilise les mêmes expressions pour obtenir l'expression de \vec{AB'} en fonction de \vec{AC}:
D'où,
arnaud4000 a écrit:J'avoue que la question 4 me semble encore plusdifficile car C' est en dehors du triangle ABC ce qui complique singulièrement les choses à me yeux

Pour la question 4), ce nest pas plus compliqué.
On commence par décomposer le vecteur
Jai marqué les vecteurs sur la figure ci-dessus.
Tiens, bonne surprise, il y a déjà dans cette expression les vecteurs
A toi de continuer en cherchant à faire disparaitre
Faisons vite:
4)
Onfait disparaitre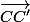 de l'expression en utilisant la relation de l'énoncée.
de l'expression en utilisant la relation de l'énoncée.
On trouve alors

5.)
Les points B, B' et C' sont alignés.
Je l'ai démontré en trouvant une relation comme celle de la question 2) :

Mais on peut en trouver une autre, liant par exemple directemetn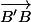 et
et 
6.) a)
J'ai trouve que
Ce qui effectivement prouve que les vecteurs sont colinéaires, mais de sens opposés.
b) En décomposant de la même manière que pour les vecteurs précédents

et

c)Les droites (A'B') et (AC') ne sont pas parallèles?
Je n'est pas trouvé de rationel q et r tels que l'on obtienne:


4)
Onfait disparaitre
On trouve alors
5.)
Les points B, B' et C' sont alignés.
Je l'ai démontré en trouvant une relation comme celle de la question 2) :
Mais on peut en trouver une autre, liant par exemple directemetn
6.) a)
J'ai trouve que
Ce qui effectivement prouve que les vecteurs sont colinéaires, mais de sens opposés.
b) En décomposant de la même manière que pour les vecteurs précédents
et
c)Les droites (A'B') et (AC') ne sont pas parallèles?
Je n'est pas trouvé de rationel q et r tels que l'on obtienne:

19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

