Petite question sur un exo

[sonny 9]

bonjour à tous et merci de votre futur aide
alors voila mon exercixe:

g(x)=(x-1)ex-1

I))

1) calculer la dérivée ( c'est fait)
2) déterminer les limites ( c'est fait)
3) démontrer que l'equation g(x)=0 admet une unique solution alpha sur lR
(je n'arrive pas à résoudre cette question.)

II)

f(x)=x/(ex+1)

1) étudier les limites et préciser l'asymptote (c'est fait mais pas sur que ce soit juste)
2) montrer que l'équation y=x est asymptote à Cf en -infini ( impossible à résoudre)
3) calculer la dérivé (c'est fait) puis étudier son signe en vous servant de la question I)4)4) en déduire le tableau de varaition ( ne devrait pas poser de problèmes)

merci d'avance :happy2:

[le_fabien]

Bonsoir,
Pour 3) il faut utiliser le théorème de la bijection.
Pour 2) il faut exprimer f(x)-x en réduisant au même dénominateur et faire la limite en -inf , elle doit être égale à zéro.
Voilà. :we:

[urmnaf]

est ce que ex-1 veut dire ou juste e*x-1

[le_fabien]

est ce que ex-1 veut dire e^x-1

Oui je pense que c'est cela.

[sonny 9]

est ce que ex-1 veut dire ou juste e*x-1

cela veut dire e*x-1[/quote]
excuser moi

[sonny 9]

Bonsoir,
Pour 3) il faut utiliser le théorème de la bijection.
Pour 2) il faut exprimer f(x)-x en réduisant au même dénominateur et faire la limite en -inf , elle doit être égale à zéro.
Voilà. :we:

oui j'ai vu dans des anal bac le théorème de la bijection mais il ne figur epas dans mon cours voila le problème
merci de vos réponse si rapide

[le_fabien]

oui j'ai vu dans des anal bac le théorème de la bijection mais il ne figur epas dans mon cours voila le problème
merci de vos réponse si rapide

Vu comme la question est formulée, tu n'as pas le choix, c'est bien le théorème de la bijection a utiliser. :we:

[urmnaf]

je vais paraitre idiot mais je n'arrive pas à comprendre ce que veux dire ton e*x-1...est-ce:


ou e fois x-1 (en quel cas est ce que e est une constante?)

[sonny 9]

pouvez vous me donner une aide supplémentaire pour le théorème de la bijection. merci

[sonny 9]

c'est e^{x}-1 ( votre 2eme proposition)

[sonny 9]

Bonsoir,
Pour 3) il faut utiliser le théorème de la bijection.
Pour 2) il faut exprimer f(x)-x en réduisant au même dénominateur et faire la limite en -inf , elle doit être égale à zéro.
Voilà. :we:

j'ai trouvé f(x)-x= (-x.e*x)/(e*x+1)

je suis sur la bonne voie ?

[urmnaf]

ok (désolé pour toute cette confusion), je suis plus très à jour sur le théorème de la bijectivité mais en gros tu dois dire que 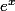réalise une bijection de sur 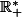et donc que toute valeur de l'ensemble d'arrivé est atteinte une et une seule fois donc il existe une seul solution à (tu dois donc au préalable te ramener à une équation de ce type)

[sonny 9]

ok (désolé pour toute cette confusion), je suis plus très à jour sur le théorème de la bijectivité mais en gros tu dois dire que réalise une bijection de sur et donc que toute valeur de l'ensemble d'arrivé est atteinte une et une seule fois donc il existe une seul solution à (tu dois donc au préalable te ramener à une équation de ce type)

ok je susi désolé mais je n'ai rien compri alors je ne dis pas sa pour que vous me rédigier la réponse mais je n'ai jamais vu cela encore donc voila... :doh: merci...

[urmnaf]

disons que tout antécédent de la fonction exponentielle admet une seule image (car elle est strictement croissante sur R), donc admet une seule solution il faut donc te ramener à une equation de cette forme.
et pour l'equation f(x)-x= (-x.e*x)/(e*x+1) que tu as trouvée il te suffit de factoriser par x pour pouvoir passer à la limite.

bon moi je vais dormir alors bonne chance :++:

[sonny 9]

disons que tout antécédent de la fonction exponentielle admet une seule image (car elle est strictement croissante sur R), donc admet une seule solution il faut donc te ramener à une equation de cette forme.
et pour l'equation f(x)-x= (-x.e*x)/(e*x+1) que tu as trouvée il te suffit de factoriser par x pour pouvoir passer à la limite.

bon moi je vais dormir alors bonne chance :++:

ok merci je vais essayer mais je n'y comprend pas grand chose à la bijection.
Est ce que vous pourriez demain m'aider pour la question 3 du II) svp. Je en serais peut ètre pas là toute l'aprem demain j'ai un rdv à l'osto donc soit le matin soit le soire je pourrais consulter vos aides. voila encor merci pour tout et de m'avoir répondu si vite.
à demain peut ètre bonne nuit au revoir