Petite question sur un calcul

[yaboo]

Bonjour,
J'ai toujours un doute pour ce genre de calcul que je dois élever au carré :



-> Pour élever cela au carré

- Est-ce que je dois utiliser l'identité remarquable (a+b)²

- Ou bien est-ce que j'ai droit de faire ceci :

[chan79]

Bonjour,
J'ai toujours un doute pour ce genre de calcul que je dois élever au carré :



-> Pour élever cela au carré

- Est-ce que je dois utiliser l'identité remarquable (a+b)²

- Ou bien est-ce que j'ai droit de faire ceci :

salut
c'est une équation à résoudre ?
Si oui, mets l'équation en entier

[Carpate]

Bonjour,
J'ai toujours un doute pour ce genre de calcul que je dois élever au carré :



-> Pour élever cela au carré

- Est-ce que je dois utiliser l'identité remarquable (a+b)²

- Ou bien est-ce que j'ai droit de faire ceci :

incomplet
avec et :

Je te laisse continuer ...

[yaboo]

L'équation est en fait :



Je n'ai aucune idée de comment résoudre ce genre d'équation alors jusque là j'ai fait :





Et pour faire disparaître la racine carré, j'ai pensé à élever encore une fois les deux membres au carré (si c'est possible)

[Carpate]

L'équation est en fait :



Je n'ai aucune idée de comment résoudre ce genre d'équation alors jusque là j'ai fait :





Et pour faire disparaître la racine carré, j'ai pensé à élever encore une fois les deux membres au carré (si c'est possible)

Avant tout calcul tu dois déterminer le domaine d'existence de cette équation
Il y a des racines carrées donc condition sur le signe du radicande ...
Tu auras ensuite à élever successivement 2 fois au carré, tache d'être rigoureux dans ce calcul

[yaboo]

Merci de la réponse :D
Je me souviens d'avoir fait un exercice de ce genre, mais jamais entendu parler de "signe du radicante" :s
Cependant, ce qui me gêne dans ce calcul, c'est le 2 dans le deuxième membre.
Faut-il que je l'ignore et détermine l'ensemble de définition sans m'en servir ?
Merci,

[Carpate]

Merci de la réponse
Je me souviens d'avoir fait un exercice de ce genre, mais jamais entendu parler de "signe du radicante" :s
Cependant, ce qui me gêne dans ce calcul, c'est le 2 dans le deuxième membre.
Faut-il que je l'ignore et détermine l'ensemble de définition sans m'en servir ?
Merci,

Le radicande, c'est l'expression algébrique sous le radical
Ici : 2x+3 et 4-x
Il faut donc qu'ils soient positifs pour que les racines carrées et l'équation soient définies

[busard_des_roseaux]

L'équation est en fait :

A priori, on doit élever deux fois au carré pour supprimer les racines....

mais , il y a une RUSE qui te permet d'élever une seule fois au carré.

comme indication, à quoi fait penser

?

[Carpate]

A priori, on doit élever deux fois au carré pour supprimer les racines....

mais , il y a une RUSE qui te permet d'élever une seule fois au carré.

commee indication, à quoi fait penser

?

Avant de penser à une astuce, il est nécessaire que yaboo détermine le domaine d'existence de l'équation, sinon il s'expose à trouver une solution inexacte ...

[busard_des_roseaux]

bof, on vérifie à la fin les solutions trouvées (méthode trash)..

[busard_des_roseaux]

bon , effectivement, Carpate demande de déterminer le domaine de définition de l'équation.

l'astuce consiste à ajouter une autre égalité auxiliaire... :doh:

[chan79]

Salut
Je sais bien qu'on fait systématiquement chercher le domaine de définition mais on peut raisonner par implication
si x est une solution alors









y'a plus qu'à résoudre cette équation du second degré et à tester les solutions avec l'équation de départ

[busard_des_roseaux]

en multipliant des deux cotés par la quantité conjuguée



en additionnant





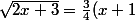la fin du calcul conduit à la "même" équation du second degré (seule solution:3)

remarque: les équations avec polynômes sont définies à un facteur près.

[yaboo]

D'accord, donc je cherche d'abord le domaine de définition :





Ce qui fait que le domaine de définition est :



Et ensuite je fais ce que chan79 a dit.
Merci à vous ! Par contre je n'ai pas très bien compris la méthode de busard_des_roseaux mais merci quand même

[busard_des_roseaux]

D=[-1,5;4]

ce n'est pas grave, la méthode de Chan marche .Ma méthode était une ruse pour n'élever qu'une seule fois au carré au lieu de deux fois.

[Carpate]

D'accord, donc je cherche d'abord le domaine de définition :





Ce qui fait que le domaine de définition est :



Et ensuite je fais ce que chan79 a dit.
Merci à vous ! Par contre je n'ai pas très bien compris la méthode de busard_des_roseaux mais merci quand même

J'écrirais plutôt