Petite équation à résoudre ....
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 17:24
par Baba » 12 Sep 2006, 17:24
Salut a tous !!
Donc voilà j'ai une petite équation à résoudre (enfin j'ai développé un truc, et je voulais savoir si ce que j'avais trouvé avait une solution, sachant que u^3+v^3=6 et uv=2 )
u^6+v^6-24=0
Merci
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 12 Sep 2006, 17:41
par abcd22 » 12 Sep 2006, 17:41
Bonsoir !
Essaie de développer
^2)
pour trouver une autre valeur pour

-
muse
- Membre Rationnel
- Messages: 845
- Enregistré le: 11 Sep 2006, 19:46
-
 par muse » 12 Sep 2006, 17:42
par muse » 12 Sep 2006, 17:42
oui y'a une solution tu sais que uv=2 donc

exprime
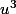
en fcontion de
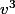
et fait des remplacement
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 17:46
par Baba » 12 Sep 2006, 17:46
Merci muse ca m'éclaire bien !!! :we:
Euh en fait non ... j'ai pas de u^3 x v^3 ...
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 12 Sep 2006, 17:57
par abcd22 » 12 Sep 2006, 17:57
Il y a des solutions à (

et

) mais pas à (

,

et

), car les deux premières conditions impliquent

.
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 18:04
par Baba » 12 Sep 2006, 18:04
Excuse moi mais je n'ai pas vraiment compris ...
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 18:12
par Baba » 12 Sep 2006, 18:12
Je crois que je vais recommencer tout depuis le début...
Ma consigne c'est:
Démontrer que si u^3 et v^3 existent, alors ils sont solutions de l'équation X²-6X+8 = 0 (sachant que auparavant j'ai déja répondu à la question: Démontrer que si u et v sont deux nombres réels tels que u^3+v^3=6 et uv=2 alors u+v est solution de l'équation x^3-6x-6=0)
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 12 Sep 2006, 18:44
par abcd22 » 12 Sep 2006, 18:44
Pour ça c'est la méthode que muse a dite (on remplace
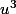
par

dans

), mais pourquoi tu parles de

alors ?
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 19:35
par Baba » 12 Sep 2006, 19:35
C'était en ayant tout développé, mais je crois que je m'étais un peu trompé ...
Au fait pour montrer qu'ils sont solutions de l'équation, faut que je remplace X par u^3+v^3 ou u^3 x v^3 ??
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 12 Sep 2006, 19:52
par abcd22 » 12 Sep 2006, 19:52
Tu pars de

, et comme

tu peux remplacer
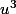
par

, puis multiplier par
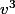
...
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 12 Sep 2006, 19:55
par nada-top » 12 Sep 2006, 19:55
pour tout équation de 2nd degré
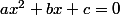
(
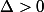
) qui admet deux solution

et

on a :
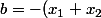)
et

alors essaye d'appliquer ça avec ton exemple .
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 20:11
par Baba » 12 Sep 2006, 20:11
En faisant ca je trouve x1=2 et x2=-2
donc ca ferait b=0 et c=-4
C'est bien cela ?
Si c'est bien cas, cela ne m'inspire rien ... :marteau: :mur:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 12 Sep 2006, 20:24
par nada-top » 12 Sep 2006, 20:24
bah non..
si
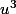
et
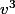
sont solution de l'équation

alors ils sont également solution de :
X +(u^3\times v^3) = 0)
tu as

et

, et on te demande s'ils sont solutions de

...ça t'inspire toujours rien ??
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 20:42
par Baba » 12 Sep 2006, 20:42
Ok j'ai compris on revient a l'équation de départ X²-6X+8=0
Donc, u^3 et v^3 sont solutions.
Maintenant, on me demande de déterminer u^3 et v^3 et d'en déduire u et v.
Comment faire ? avec delta ?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 12 Sep 2006, 20:49
par nada-top » 12 Sep 2006, 20:49
Ok j'ai compris on revient a l'équation de départ X²-6X-6=0
c'est

oui maintenant tu résous cette équation avec le descriminent , et tu en déduis u et v .
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 20:53
par Baba » 12 Sep 2006, 20:53
C'était une petite faute de frappe !!
Merci de me l'avoir fait remarquer ! :++:
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 21:04
par Baba » 12 Sep 2006, 21:04
J'ai trouvé x1=2 et x2=4
C'est bien cela ?
Si j'ai bien compris, alors u^3=2 et v^3=4
C'est bien cela ou j'ai raté un truc?
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 12 Sep 2006, 21:08
par nada-top » 12 Sep 2006, 21:08
oui c'est bon :++:
maintenant déduis-en u et v .
-
Baba
- Membre Relatif
- Messages: 215
- Enregistré le: 30 Oct 2005, 21:55
-
 par Baba » 12 Sep 2006, 21:13
par Baba » 12 Sep 2006, 21:13
Pour le déduire faut faire quoi ?
Une racine cube ?!?!! :hein:
-
nada-top
- Membre Rationnel
- Messages: 661
- Enregistré le: 17 Juil 2006, 00:35
-
 par nada-top » 12 Sep 2006, 21:16
par nada-top » 12 Sep 2006, 21:16
oui bien sur , une racine cubique.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
