Petit problème

[atic900]

bonjour,

j'ai un petit problème avec une expression à factoriser, au premier abord elle parait simple mais cela se complique par la suite. dites moi juste d'après vos résultats si cette expression est factorisable ou pas : (2x-3)(x+2)+(x+2)(x²+1) et moi je me retrouve avec ce résultat : (x+2)(x²+2x-2) et pour moi impossible d'aller plus loin. Quand pensez vous ?

[biss]

c'est deja bien non ?

[atic900]

[quote="biss"]c'est deja bien non ?[/QUO

(x²+2x-2) me fait penser à une identité remarquable, j'ai l'impression qu'il y a un piège

[biss]

[chaa13]

Salut,
Si un jour tu es bloqué sur la factorisation d'une expression du genre :
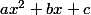
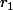
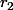
Calcul les deux racines et , et après tu peux factoriser comme cela

[atic900]

ok, merci à tous les deux c'est sympa

[atic900]

donc juste pour confirmation, la forme factorisée de (x+1)²-3 c'est :

=(x+1)²-(v3)²
=[(x+1)-(v3)][(x+1)+(v3)]

[chaa13]

Oui .

[atic900]

impeccable merci