[B]petit exo congruence...aidez moi!!!!!svp[/B]

par **izamane95** » 29 Oct 2006, 16:51

:dingue: Bonjour voilà l'énnoncé:
démontrer que pour tout n naturel ,le nombre An = n4^n+1 - (n+1)4^n +1 est divisible par 9
n'ésitez pas à me donner vous idées ça pourra m'aider....!! :space:

par **izamane95** » 29 Oct 2006, 16:56

j' ai pensé à démontrer que An = 0(mod9) pour cela il me fout calculer les restes dans la division par 9 de chacun des termes .
et donc pour commencer,il fout que je calcule ces restes pour 4^n
notons rn le reste de la division de 4^n par 9
mais je me bloque à cette étape : 4^n = -5^n(mod9)
.................... :help:

par **Quidam** » 29 Oct 2006, 16:56

izamane95 a écrit::dingue: Bonjour voilà l'énnoncé:
démontrer que pour tout n naturel ,le nombre An = n4^n+1 - (n+1)4^n +1 est divisible par 9
n'ésitez pas à me donner vous idées ça pourra m'aider....!! :space:

Enoncé ambigu !

divisible par 9
ou

divisible par 9

J'ai une préférence pour la première formule, bien sûr, mais je déteste chercher sur un problème qui n'existe pas !

Alors, mets donc des parenthèses là où c'est nécessaire !

par **izamane95** » 29 Oct 2006, 16:59

exusez moi ....!!
c'est plutot la première formule

par **izamane95** » 29 Oct 2006, 17:06

par **Quidam** » 29 Oct 2006, 17:32

izamane95 a écrit:

Observe l'évolution de

à mesure que n varie. Tu constateras que

Par conséquent :

De même

et de façon générale,

quel que soit k entier positif !
Fais la même constatation sur (3n-1) !
Finalement, tu montreras que tu peux te contenter de vérifier le théorème pour n=0,1, et 2 !

Il y a probablement d'autres méthodes plus astucieuses, mais elle ne m'ont pas sauté aux yeux...

par **izamane95** » 29 Oct 2006, 17:52

désolé quiadam ;j'arrive pas à suivre votre méthode ,moi j'aime bien partir de zéro et dire qu'il suffit de démontrer que :

pour cela il me faut calculer les restes dans la division par 9 de chacun des termes , et donc ,pour commencer , je calcule ces restes pour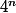

(ceux de

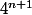s'en déduisent facilement
aprés je note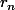

le reste de la division de

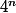par 9
mais je me bloque à cette étape là : comme

donc

pouvez vous m'aidez à résoudre le pb en utilisant ma méthode...???SVP :help:

par **izamane95** » 29 Oct 2006, 18:05

EN FAIT JE VEUX CALCULER

par **izamane95** » 29 Oct 2006, 18:09

pour

on a

donc

(je suis pas sur . est ce que c'est vrais????!!!)

par **Quidam** » 29 Oct 2006, 18:17

izamane95 a écrit:pour on a donc
(je suis pas sur . est ce que c'est vrais????!!!)

Tu vois quelque chose ?

par **izamane95** » 29 Oct 2006, 18:26

nn
mais ensuit je prouve que pour chacun des cas suivats : n= 3p, n= 3p+1 , n=3p+2

par **izamane95** » 29 Oct 2006, 18:34

et ça j'arrive pas à le démontrer

par **Quidam** » 29 Oct 2006, 19:40

izamane95 a écrit:nn
mais ensuit je prouve que pour chacun des cas suivats : n= 3p, n= 3p+1 , n=3p+2

Tu poses n=3p+k avec

Cas k=0 :

Cas k=1 :

Cas k=2 :

Terminé !

par **mostdu95** » 30 Oct 2006, 14:05

pouvez vous m'expliquer la derniere ligne (plutot je ne connais pas le symbole :dingue: qui est entre 9 et 16 et entre 5 et 16....?????!! :soupir2:

par **izamane95** » 30 Oct 2006, 14:12

:hey: mon non plus

par **Quidam** » 30 Oct 2006, 15:52

mostdu95 a écrit:pouvez vous m'expliquer la derniere ligne (plutot je ne connais pas le symbole :dingue: qui est entre 9 et 16 et entre 5 et 16....?????!! :soupir2:

Désolé ! Il s'agit du signe "multiplier par", soit " x ". Il est d'usage, dans les logiciels de symboliser la multiplication par l'astérisque " * ". Evidemment, si j'écris ça dans une formule LaTex, ça marche pas !

C'est corrigé !

par **izamane95** » 30 Oct 2006, 16:26

ahhhhhhhhhhhhhh..ok :euh:

par **izamane95** » 30 Oct 2006, 16:46

:crunch: :k2k: mais pourqoui dans chaque ligne vous mettez le modulo 9
car en fait on a

donc on veut montrer que

moi je trouve plutot que

comme

donc si k=1

dans le dernier cas je comprend pas pourquoi c'est congru à 0(9)

par **Quidam** » 30 Oct 2006, 17:18

izamane95 a écrit:mais pourqoui dans chaque ligne vous mettez le modulo 9
car en fait on a

Ben, ça ne mange pas de pain ! Si a=b alors a =b (9) (c'est la réciproque qui n'est pas vraie !) C'est vrai que je l'ai mis partout par pure paresse.
Jusque :

ce n'était pas la peine d'écrire "modulo 9" car c'est une égalité entre entiers, dans N. Mais quand je passe à :

...je suis obligé de mettre "modulo 9" car j'ai fait disparaître le

qui n'est absolument pas égal à 1 mais qui l'est "modulo 9".

izamane95 a écrit:donc si k=1

donc si k=1

izamane95 a écrit:dans le dernier cas je comprend pas pourquoi c'est congru à 0(9)

Cas k=2 :

par **khamaths** » 30 Oct 2006, 17:35

bonsoir
tu peux remarquer que:

4^3k =1[9]
4^(3k+1)=4[9]
4^(3k+2)=-2[9]
tu peux discuter suivant n:
* si n=3k .... tu remplaces dans l'expression et tu trouveras le resultat.
*si n=3k+1.....
*si n=3k+2...

[B]petit exo congruence...aidez moi!!!!!svp[/B]

[B]petit exo congruence...aidez moi!!!!!svp[/B]

Qui est en ligne