entropik a écrit:ah oui juste c'est bizarre
Si n est impaire ca se demontre facilement car C(p,n) = C(n-p,n) (c'est le caractere symetrique des combinaisons, il y a autant de manieres de choisir p elements dans un ensemble a n elements que d'en choisir n-p dans un ensemble a n elements, c'est logique vu que de choisir p elements ca revient a ne pas en choisir n-p. Donc le nombre de maniere differente d'en prendre p vaut bien le nombre de maniere differente de ne pas en prendre n-p qui vaut le nombre de maniere differente d'en prendre n-p forcement...)
De plus n-p et p sont de parités differentes si n est impaire.
On a alors si p est paire, n-p est impaire. si p est impaire, n-p est paire.
Du coup ca revient a sommer deux a deux les (-1)^p*C(p,n) + (-1)^(n-p)*C(n-p,n) qui sont des nombres opposés car si p est paire et n est impaire (-1)^p et (-1)^(n-p) valent 1 et -1 ou -1 et 1. Donc (-1)^p*C(p,n) + (-1)^(n-p)*C(n-p,n) = 0. tu les sommes ainsi deux par deux de 0 à n et ta somme vaut 0...
Pour un n paire c'est un peu plus compliqué, mais ca se demontre aussi:
Grace a la relation de Pascal C(p,n)=C(p,n-1)+C(p-1,n-1).
Si n paire les termes symetriques ont cette fois le meme signe donc:
somme((-1)^kC(k,n))= somme C(2k,n) - somme (C(2k+1,n)
grace au triangle de Pascal ca donne:
somme [C(2k,n-1)+C(2k-1,n-1)] - somme [C(2k+1,n-1)+C(2k,n-1)]
= Somme(C(k,n-1)) - Somme(C(k,n-1)) =0
.
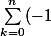^k C\(k\\n\))
. Ainsi, si a= -1 il faudrait que
mais dans ce cas b=1 et le binôme serait égal à 0 alors est-ce que cela à un sens? Sinon que peut on faire?