Bonsoir, je reviens avec un autre exercice de probabilité.
Je pense savoir comment faire, mais je suis pas sûr de totalement saisir ce qu'on me demande et je trouve ma méthode très longue (donc probablement pas la bonne):
"On choisit par hasard un entier n entre 1 et 4. Ensuite, on lance une pièce n fois. On note N le nombre de piles obtenues.
Donner la loi de N et E(N)"
Donc je vois bien qu'on a un cas où il faut utiliser la loi binomiale, mais par "donner la loi de N" on me demande juste de calculer les probabilités pour toutes les valeurs de N? (et pour tout n)
Ca me fait 1+2+3+4 probabilités à calculer avec la formule dont certaines assez lourdes quand n=4. Et aussi ça fait 4 tableaux. Je trouve ça assez long, se pourrait-il que je fasse complètement fausse route?
Merci d'avance de votre aide.
Petit exercice de probas
9 messages
- Page 1 sur 1
Re: petit exercice de probas
par samoufar » 31 Mai 2016, 21:32
Bonsoir,
Détermination de la loi de
:
Déterminer la loi de revient à trouver )
ou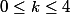 
, ce qui n'a a priori pas de rapport avec le choix de 
.
Or dans notre situation, disons pour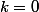
(le plus dur avec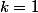 
),
 = \mathbf{P}(N=0 \cap n=1)+\mathbf{P}(N=0 \cap n=2)+\mathbf{P}(N=0 \cap n=3)+\mathbf{P}(N=0 \cap n=4))
Là tu appliques tes lois binomiales, et ça ne devrait pas être compliqué à calculer. C'est long, certes, mais il ne semble pas y avoir de moyen plus efficace (sauf si la pièce est équilibrée, auquel cas tu as par exemple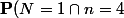=\mathbf{P}(N=3\cap n=4))
).
Remarque : On ne peut pas avoir
, et donc par exemple
 = 0 + \mathbf{P}(N=4 \vert n=4))
Détermination de la loi de)
:
Elle est donnée par la formule
=\displaystyle\sum_{k=0}^4 k\cdot\mathbf{P}(N=k))
.
Détermination de la loi de
Déterminer la loi de
Or dans notre situation, disons pour
),Là tu appliques tes lois binomiales, et ça ne devrait pas être compliqué à calculer. C'est long, certes, mais il ne semble pas y avoir de moyen plus efficace (sauf si la pièce est équilibrée, auquel cas tu as par exemple
Remarque : On ne peut pas avoir
Détermination de la loi de
Elle est donnée par la formule
Modifié en dernier par samoufar le 01 Juin 2016, 12:20, modifié 1 fois.
Re: petit exercice de probas
par Pseuda » 01 Juin 2016, 11:23
Bonjour,
 =\sum{P((N=k)\cap(n=i))}=\sum{P(n=i)*P(N=k|n=i)})
(somme pour i allant de 1 à 4)
)
: facile
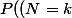|(n=i)))
: il n'y a pas d'autre moyen que la loi binomiale. 
(somme pour i allant de 1 à 4)
Modifié en dernier par Pseuda le 01 Juin 2016, 11:27, modifié 1 fois.
Re: petit exercice de probas
par Tir McDohl » 01 Juin 2016, 11:26
Je vois, du coup moi je comptais séparer les choses avec les valeurs de n, alors qu'il vaut mieux le faire avec les valeurs de k.
J'ai commencé mais je bloque à un moment:
= \begin{pmatrix} 1 \\ 0 \end{pmatrix} \times (\frac{1}{2})^0 \times (\frac{1}{2})^1 = 1 \times 1 \times \frac{1}{2} = \frac{1}{2})
= \begin{pmatrix} 2 \\ 0 \end{pmatrix} \times (\frac{1}{2})^0 \times (\frac{1}{2})^2 = 1 \times 1 \times \frac{1}{4} = \frac{1}{4})
 = 1 \times 1 \times \frac{1}{8} = \frac{1}{8})
 = 1 \times 1 \times \frac{1}{16} = \frac{1}{16})
= \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} = \frac{8}{16} + \frac{4}{16} + \frac{2}{16} + \frac{1}{16} = \frac{15}{16})
= \begin{pmatrix} 1 \\ 1 \end{pmatrix} \times (\frac{1}{2})^1\times (\frac{1}{2})^0 = 1 \times \frac{1}{2} \times 1 = \frac{1}{2})
= \begin{pmatrix} 2 \\ 1 \end{pmatrix} \times (\frac{1}{2})^1 \times (\frac{1}{2})^1 = 2 \times \frac{1}{4} = \frac{1}{2})
= \begin{pmatrix} 3 \\ 1 \end{pmatrix} \times (\frac{1}{2})^1 \times (\frac{1}{2})^2 = \frac{3}{2} \times \frac{1}{4} = \frac{3}{8})
= \begin{pmatrix} 4 \\ 1 \end{pmatrix} \times (\frac{1}{2})^1 \times (\frac{1}{2})^3 = 2 \times \frac{1}{8} = \frac{1}{4})
 = \frac{1}{2} + \frac{1}{2} + \frac{3}{8} + \frac{1}{4} = \frac{4}{8} + \frac{4}{8} + \frac{3}{8} + \frac{2}{8} = ???)
Comme vous pouvez le voir, ça donne une probabilité supérieure à 1, ce que je ne comprend pas vu qu'avec 1 on a déjà la certitude que ça va arriver (et qu'on peut pas l'avoir de toute façon). J'ai cherché des erreurs de calcul et je ne trouve pas...
J'ai commencé mais je bloque à un moment:
Comme vous pouvez le voir, ça donne une probabilité supérieure à 1, ce que je ne comprend pas vu qu'avec 1 on a déjà la certitude que ça va arriver (et qu'on peut pas l'avoir de toute façon). J'ai cherché des erreurs de calcul et je ne trouve pas...
Re: petit exercice de probas
par Pseuda » 01 Juin 2016, 11:30
Hum, il faut ajuster la formule avec les (voir mon message plus haut, passé avant le tien).
Il me semble préférable d'effectuer les calculs en fixant d'abord les valeurs pour n, puis pour k (cela ne change rien au résultat, mais c'est plus logique).
Il me semble préférable d'effectuer les calculs en fixant d'abord les valeurs pour n, puis pour k (cela ne change rien au résultat, mais c'est plus logique).
Re: petit exercice de probas
par Tir McDohl » 01 Juin 2016, 12:03
Ah oui désolé. Donc je multiplie chacun des éléments de ma somme par la probabilité du n?
Pour n j'avoue que vu que j'ai commencé avec cet ordre et que ça revient au même, j'ai pas la force de tout changer xD. Du coup:
 = 1/4)
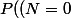) = \frac{1}{4} \times \frac{1}{2} + \frac{1}{4} \times \frac{1}{4} + \frac{1}{4} \times \frac{1}{8} + \frac{1}{4} \times \frac{1}{16} = \frac{1}{8} + \frac{1}{16} + \frac{1}{32} + \frac{1}{64} = \frac{8}{64} + \frac{4}{64} + \frac{2}{64} + \frac{1}{64} = \frac{15}{64})
? des trucs comme ça?
edit: aussi, on me demande de donner la "définition d'une mesure probabilité" dans une question de cours, mais même sur internet je ne trouve pas exactement. Il faut juste dire qu'on est dans un espace probabilisé)
avec P entre 0 (échec assuré) et 1 (succès assuré) ?
Merci d'avance.
Pour n j'avoue que vu que j'ai commencé avec cet ordre et que ça revient au même, j'ai pas la force de tout changer xD. Du coup:
? des trucs comme ça?
edit: aussi, on me demande de donner la "définition d'une mesure probabilité" dans une question de cours, mais même sur internet je ne trouve pas exactement. Il faut juste dire qu'on est dans un espace probabilisé
Merci d'avance.
Re: petit exercice de probas
par Pseuda » 01 Juin 2016, 18:03
Oui c'est ça.
Remarque : tu peux mettre 1/4 en facteur .... pour simplifier les calculs.
Pour la définition d'une probabilité, en quelle classe es-tu ?
Tu as dû voir qu'une mesure de probabilité vérifie ces 3 axiomes :
la proba de tout événement est comprise entre 0 et 1,
la proba de l'univers = 1,
la proba de la réunion de 2 événements incompatibles est obtenue en additionnant la proba des 2 événements.
Remarque : tu peux mettre 1/4 en facteur .... pour simplifier les calculs.
Pour la définition d'une probabilité, en quelle classe es-tu ?
Tu as dû voir qu'une mesure de probabilité vérifie ces 3 axiomes :
la proba de tout événement est comprise entre 0 et 1,
la proba de l'univers = 1,
la proba de la réunion de 2 événements incompatibles est obtenue en additionnant la proba des 2 événements.
Re: petit exercice de probas
par Tir McDohl » 01 Juin 2016, 19:02
Merci.
Pour le second truc non en fait c'était juste une histoire de terminologie, le "mesure" dans mesure de probabilité me faisait penser qu'on me demandait autre chose. C'est toujours ça le problème avec les questions de cours trop théoriques on sait jamais trop à moins connaitre par cœur les termes précis. Je suis tjrs plus à l'aise en application.
Bon du coup tous mes problèmes sont réglés l'exos devrait aller tout seul. J'en ai fait d'autres sur les lois uniformes et geométriques mais ça me semblait plus simple donc je pense être ok. Merci encore.
Pour le second truc non en fait c'était juste une histoire de terminologie, le "mesure" dans mesure de probabilité me faisait penser qu'on me demandait autre chose. C'est toujours ça le problème avec les questions de cours trop théoriques on sait jamais trop à moins connaitre par cœur les termes précis. Je suis tjrs plus à l'aise en application.
Bon du coup tous mes problèmes sont réglés l'exos devrait aller tout seul. J'en ai fait d'autres sur les lois uniformes et geométriques mais ça me semblait plus simple donc je pense être ok. Merci encore.
Re: petit exercice de probas
par zygomatique » 02 Juin 2016, 18:09
salut
vu que n = 4 est petit et après avoir bien préciser ce qu'est la loi de N sachant n je ferais un tableau dont seule la moitié est remplie
je te laisse compléter la dernière colonne .... et calculer proprement P(N = k) pour k variant de 0 à 4
.....
vu que n = 4 est petit et après avoir bien préciser ce qu'est la loi de N sachant n je ferais un tableau dont seule la moitié est remplie
- Code: Tout sélectionner
N \ n 1 2 3 4
0 1/2 1/4 1/8 1/16
1 1/2 1/2 6/8
2 / 1/4 6/8
3 / / 1/8
4 / / / 1/16
je te laisse compléter la dernière colonne .... et calculer proprement P(N = k) pour k variant de 0 à 4
.....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
9 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 86 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :