Petit bloquage niveau 2nd

par **nayar** » 10 Sep 2006, 15:55

bonjour a tous !
j'ai besoin d'un peu d'aide svp
rac=racine

Soit A=rac(6-2rac5)-rac(6+2rac5).
Calculer A^2 puis déduisez-en la valeur de A.

donc moi j'ai commencé et je bloque a :
rac(56-24rac5)+rac(56+24rac5)-8
mais je me suis peut-étre trompé dans les calcule avant...

merci de m'aidé

par **nayar** » 10 Sep 2006, 16:10

svp ca doit pas étre bien dur pour vous ...
:help:

par **Clembou** » 10 Sep 2006, 16:21

Bonjour,

Pour la formule tex, c'est comme ça

Détail du calcul

par **nayar** » 10 Sep 2006, 16:25

mais moi je sais pas comment vous fétes pour la formule tex
et aidé moi svp

par **Clembou** » 10 Sep 2006, 16:27

nayar a écrit:mais moi je sais pas comment vous fétes pour la formule tex
et aidé moi svp

La solution est en haut

Pour la forumle TeX, ce n'était pas grave, c'est pour voir l'opération à faire.

par **nayar** » 10 Sep 2006, 16:33

oooooooo merci
jme suis cassé la téte pour rien ....
c'était tt simple...
merci beaucoup

par **nayar** » 10 Sep 2006, 17:10

Et j'aie une autre question totalement différente :

a et b sont deux réels tel que : a ranger dans l'orde croissant les nombres suivants :

a/(b-1) ; a/b ; (a-1)/(b-1) ; (a-1)/b .

donc moi je pense que ca donne :

a/(b-1) < (a-1)/(b-1)
c'est ca ?
et comment je fait pour le démontrer ??

:help: svp

par **nayar** » 10 Sep 2006, 17:27

ya personne pour m'aidé ?? c'est juste pour me dire si c'est juste et coment il faut faire pour le démontrer ...

par **Clembou** » 10 Sep 2006, 17:35

nayar a écrit:Et j'aie une autre question totalement différente :

a et b sont deux réels tel que : a <ou= b < 0
ranger dans l'orde croissant les nombres suivants :

a/(b-1) ; a/b ; (a-1)/(b-1) ; (a-1)/b .

donc moi je pense que ca donne :

a/(b-1) < (a-1)/(b-1) <ou= a/b < (a-1)/b

c'est ca ?
et comment je fait pour le démontrer ??

:help: svp

Si a = b, on a donc

<

=

<

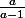
Donc c'est très judicieux d'avoir mis un < ou = entre deux expressions.

Après si tu veux démontrer. (b-1) est un dénominateur et si on agrandit la valeur du dénominateur, on a une fraction d'une valeur plus petite. (exemple :

).

Même chose pour (a-1) : si on agrandit la valeur du numérateur on a une faction d'une valeur plus grande.

par **nayar** » 10 Sep 2006, 17:55

ok merci beaucoup
je vais pouvoir allé dormir tranquille cette nuit
:we:

Petit bloquage niveau 2nd

petit bloquage niveau 2nd

Qui est en ligne