La période d'une fonction

[Black Jack]

Salut,

Ne pas trop se casser la tête ...
L'énoncé court sur plusieurs sites ... mais avec une différence probablement due à une erreur ici.

Partout ailleurs, il s'agit de f(x+1) = 1/(1 - f(x))

[chan79]

Quelqu'un aurait-il trouvé une fonction f qui vérifie cette égalité ?

[Ben314]

Si tu cherche une "jolie" fonction vérifiant je peut te proposer celle là :
où et

[chan79]

et une fonction de dans ?

[Ben314]

Des fonction continues et définies sur R tout entier vérifiant le bidule, c'est assez clair qu'il n'y en a pas.

[Ben314]

où et

De plus, sauf erreur, si on prend de module égal à 1 alors la fonction çi dessus est bien à valeur réelle (mais pas définie sur R tout entier) :

[chan79]

OK merci. Avec k=i, ça fait la courbe ci-dessous, qui rappelle la tangente.

wolfram propose un truc du même genre, à valeurs dans , apparemment.

[Ben314]

En fait faire varier k (en le gardant de module =1), ça sert pas à grand chose , ça fait que translater la courbe.
Et après calcul (où je me suis planté 5 fois...), ça donne ça :

Avec phi quelconque (mais qui ne fait que translater la courbe)

[chan79]

Bien vu !
Avec ça donne


n'est pas définie si est de la forme 1+3k (k entier )
A un changement de repère près, c'est la fonction tangente.

[Carpate]

Bonjour,
Toujours avec , je trouve une incohérence entre les résultats obtenus avec les 2 méthodes citées plus haut :
1) Par calcul algébrique simple, on obtient
2) En utilisant la méthode de Ben314 avec la matrice A codant la transformation homographique soit
A a pour polynôme caractéristique et pour valeurs propres qui ne sont pas 2 des racines troisièmes de l'unité.
mais égal à
On aurait donc par cette méthode f(x+3)=-f(x) et f(x+6)= f(x)
Qui aurait une explication ?

[Ben314]

L'explication est à la fois simple... et compliqué...

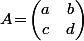
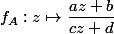
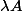
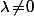
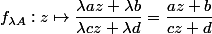
La vision "simple", c'est tout bêtement que, si à la matrice (inversible) tu associe l'homographie alors à la matrice () tu associe ce qui ne change rien.
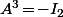
Donc par exemple le fait que signifie bien que .

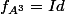
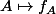
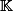
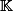
La vision "compliquée", ça consiste à dire que le morphisme de dans le groupe des homographies de dans , il est évidement surjectif, mais pas injectif et que plus précisément, son noyau, c'est l'ensemble des matrices diagonales (non nulles), c'est à dire en fait le centre de (i.e. les matrices qui commutent avec toute les autres).
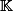
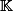
Donc le premier théorème d'isomorphisme te dit groupe des homographies de dans il est isomorphe au quotient de par son centre. Quotient que, dans la littérature, on note avec un P comme "projectif" vu qu'en fait, regarder les matrices à multiplication par un scalaire prés, ça signifie qu'on fait opérer les matrices non pas sur les vecteurs, mais sur les sous espaces vectoriels de dimension 1 de l'espace (si tu multiplie la matrice A par lambda, ca change A.V pour un vecteur V donné, mais ça ne change pas A.vect{V}) et comme l'ensemble des sous espaces de dim 1 d'un espace vectoriel, c'est justement la définition de l'espace projectif associé, ça signifie que , il agit "naturellement" sur l'espace projectif de dimension 1 sur (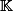i.e. sur l'ensemble des droites vectorielles de ).
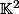
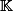
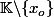
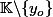
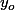
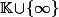
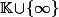
Et là où on retombe sur un truc on ne peut plus "naïf", c'est qu'on retrouve le truc assez trivial consistant à dire qu'un homographie sur , plutôt de dire que c'est une bijection de sur (ou le et le dépendent de l'homographie donc foutent la merde quand on compose des homographies), ben vaut 100 fois mieux les voire comme des bijections de sur lui m\^eme. Et bien sûr, , c'est en fait l'espace projectif de dimension 1 sur ...

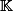
Bref, comme d'hab. : deux vision du même bidule : une assez "terre à terre" et une autre bien plus théorique, mais qui explique très précisément le "pourquoi du comment" du bidule (et comment ça se généralise naturellement en dimension quelconque avec la notion d'affinitées)

[Carpate]

Merci

[Ben314]

Si tu cherche une "jolie" fonction vérifiant je peut te proposer celle là :
où et

Et en fait, en regardant d'un tout petit peu plus prêt, LES (i.e. toutes) solutions de en fait, c'est les fonctions de la forme où et est une fonction 1-périodique.
Et est une fonction à valeur réelle ssi est à valeur dans le cercle trigo donc bien évidement constante égale à 1, ça marche, mais avec entier quelconque, ça marche aussi (et ça fait bien sûr une fonction tout aussi "régulière" là où elle est définie)