Pbm fonction derivée

[GTO59]

1.soit I=]0;+oo[ et u et v les deux fonctions définies sur I par u(x)=2x-1 et v(x)=
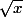
a) montrer que u et v sont derivable sur I et determiner leur derivée.
b) soit f la fonction definie sur I par f(x)=(2x-1)
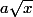
Montrer que f est dérivable sur I et que peut s'ecrire sous la forme + où a et b sont 2 constantes que l'on determinera.

bon dans l'exo j'ai tout reussi mais je narrive pas a faire les truc souligné en gras
on ma di pour ce qui est souligné dans le b quil fallait utiliser les taux de variation mais je c pas c avec quelle nombre.
merci d'avance :we:

[titine]

Il faut revenir à la définition :
Une fonction f est dérivable sur I si, pour tout x de I, la limite quand h tend vers 0 de [f(x+h)-f(x)]/h existe.

[titine]

Pourquoi avoir poster 2 messages identiques ?
Pour que nous puissions t'aider efficacement, prends ton cours et recopie nous la définition d'une fonction dérivable que ton prof vous a donné. On partira de là.

En fait en remontant les posts, je me suis aperçu que tu avais posé le même exercice au moins 5 fois ....
Quand tu as démarré une discussion il faut continuer sur celle ci, sinon nos réponses ne pourront pas se compléter et tu n'y comprendras rien !
En plus tu te fous un peu de nous car on prend du temps pour te donner une solution alors que quelqu'un te l'a déja donnée ...