le b. est effectivement la question la plus dure
il faut utiliser la relation de Chasles et une caractérisation du centre de gravité
Connais-tu cette caractérisation ?
* si
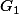
est centre de gravité de DEF alors
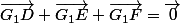
Si oui, c'est très simple, tu utilises Chasles en introduisant le point H dans chacun des 3 vecteurs.
Si non (je te conseille toutefois d'apprendre la caractéristation précédente , bien utile), c'est un peu plus long
*
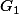
est au 2/3 des médianes.
Appelle I le milieu de [EF]
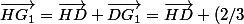\vec{DI})
J'espère au moins que tu connais cette caractérisation du milieu
* si I est milieu de [EF] alors
(\vec{DE}+\vec{DF})
) ?
tu remplaces, tu utilises Chasles en introduisant le point H et tout marche très bien
Si tu ne connais pas la caractérisation précédente ... (fais-toi une fiche où tu noteras et apprendras les caractérisations que je t'ai données!!!)
il ne te reste plus qu'à continuer à utiliser la relation de Chasles et écrire
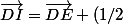\vec{EF})
, à remplacer dans ton expression et à utiliser Chasles en glissant le point H dans tous les vecteurs présents
Bon courage

