Passer du quatrieme au 2eme degre

par **clems421** » 05 Oct 2008, 14:22

bonjour, je dois rendre un DM de maths mardi et il y a un exo sur lequel je bloque . voici l'énoncé:
On se propose de montrer qu'il existe un polynome P tel que, pour tout réel de x, x^4+6x^3+11x²+6x+1 = [P(x)]²
Quel doit etre le degre de P?
Ecrire la forme generale d'un tel polynome
Determiner alors un tel polynome P
Conclure
Est-ce-quue quelqu'un pourrait m'aider?
Je vous remercie d'avance.

par **Skullkid** » 05 Oct 2008, 14:24

Bonjour, si P est de degré d, quel est le degré de P² ?

par **Anonyme** » 05 Oct 2008, 14:32

Je viens de poster le même problème (enfin pas les mêmes valeurs mais c'est aussi du 4ème degrés.)

Je vois le degré de

mais je ne vois où tu veux en venir Skullkid.

par **Skullkid** » 05 Oct 2008, 14:43

C'est pour répondre à la question "quel doit être le degré de P ?". On sait que P² est de degré 4, donc si on connaît le degré de P² en fonction de celui de P, on peut en déduire le degré de P.

Bon, comme le laisse supposer le titre du sujet, P est de degré 2, on peut donc écrire sa forme générale, l'élever au carré et identifier les coefficients de P² avec ceux de

.

par **Anonyme** » 05 Oct 2008, 14:49

Je ne vois pas ce que c'est que la forme générale. Mais normalement il faut f

par **Anonyme** » 05 Oct 2008, 14:52

Je ne vois pas ce que c'est que la forme générale. Mais normalement il faut factoriser P par

et ensuite poser un u=... et on devrait normalement obtenir

(il peut avoir des coefficients devant les u) et uk suffit ensuite de chercher les solutions de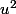

et de u. (Enfin j'avais fait cette méthode dans un exercice ou l'équation était égale à 0. Donc niquelle pour trouver les solutions (surtout que le u nous était donnez.)

par **Skullkid** » 05 Oct 2008, 14:54

Par quoi est défini un polynôme de degré 2 ?

par **Anonyme** » 05 Oct 2008, 15:18

Un polynôme du 2nd degré est défini sur R.

par **Skullkid** » 05 Oct 2008, 15:20

Attention, j'ai pas dit "sur quoi" mais "par quoi" !

La réponse que j'attendais est "par 3 coefficients". La forme générale d'un polynôme de degré 2 c'est P(x) = ax² + bx + c. Trouver P c'est trouver a, b et c.

par **Anonyme** » 05 Oct 2008, 15:34

Ah oui ok mais avec le 4ème degrés je vois pas du tout comment y parvenir.

par **Skullkid** » 05 Oct 2008, 15:39

Tu suis la méthode que j'ai indiquée plus haut, tu sais que P(x) = ax² + bx + c. Donc P(x)² vaut ...

Or

. A partir de là tu peux déduire a, b et c.

par **Anonyme** » 05 Oct 2008, 15:55

Donc

(mais je nais ni de d ni de e ^^) donc je vois pas très bien comment faire, mais je préfère me concentré sur mon problème (http://www.maths-forum.com/showthread.php?t=70220) qui est un peut différent de celui-ci ^^ (donc au passge si tu veux venir ^^")

par **Skullkid** » 05 Oct 2008, 16:04

P n'est pas de degré 4 ! Il suffit de calculer P(x)² et d'identifier les coefficients...

par **Anonyme** » 05 Oct 2008, 16:09

Ah ui j'ai fait un faute de frappe:

par **Anonyme** » 05 Oct 2008, 16:17

J'ai trouvé (je pense^^):

Donc
a=1
b=3
c=1

par **Skullkid** » 05 Oct 2008, 16:21

-Scofield- a écrit:Ah ui j'ai fait un faute de frappe:

Non, P(x)² = (ax² + bx + c)², il suffit de développer.

-Scofield- a écrit:

Donc
a=1
b=3
c=1

Oui, c'est la bonne réponse.

Passer du quatrieme au 2eme degre

passer du quatrieme au 2eme degre

Qui est en ligne