Pas d'idée pour la résolution ??

par **superphyl** » 13 Oct 2012, 15:14

Je ne trouve pas le commencement d'un début d'idée pour résoudre ce DM....
Quelqu'un peut il m'aider ? Merci.

Trouver l'ensemble des points décrits par le sommet de la parabole de la fonction

, avec b appartenant à

a) Formuler une conjecture appuyée sur l'utilisation d'un tableur
b) Essayer de la démontrer

par **Dlzlogic** » 13 Oct 2012, 15:28

Bonjour,
Qu'est-ce que ça donne avec un tableur ?

par **superphyl** » 13 Oct 2012, 15:42

Dlzlogic a écrit:Bonjour,
Qu'est-ce que ça donne avec un tableur ?

C'est bien là le problème, je n'ai jamais rencontré ce style de méthode.
Après une petite recherche sur internet j'ai rentré la formule et les différentes valeurs de b de -20 à 20 et ça me donne plusieurs paraboles qui ont l'air d'avoir leur sommet commun...

par **Dlzlogic** » 13 Oct 2012, 16:12

Savez-vous vous servir d'un tableur ?

par **superphyl** » 13 Oct 2012, 16:46

Voilà le résultat que j'obtiens en utilisant un tableur en fonction des valeurs différentes de x et de b.

par **superphyl** » 13 Oct 2012, 17:42

J'en ai deduit qu'avec les valeurs de b comprise entre + et - l'infini la valeur de x est comprise entre 2 et + l'infini ...
Qu'en pensez vous ?

par **annick** » 13 Oct 2012, 17:51

Bonjour,
sur tes courbes tracées avec le tableur, il faudrait que tu marques bien chaque sommet et que tu essayes de les relier pour voir quel type de courbe ça te donne.
Ensuite pour démontrer algébriquement, il faut que tu trouves les coordonnées de ton sommet S en fonction de b, puis que tu exprimes yS en fonction de xS en éliminant les b. Tu auras alors l'équation d'une courbe qui est celle sur laquelle se "promène" ton sommet et qui devrait correspondre à ce que tu avais aperçu avec le tableur.

par **superphyl** » 13 Oct 2012, 18:04

Bonjour, effectivement nous sommes arrivés à trouver visuellement que la courbe qu'on nomme g(x)=

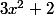
est bien celle qui réunit le sommet des courbes prenant en compte toutes les valeurs de b mais on se sait par le "montrer" algébriquement.
Ensuite nous n'arrivons pas à exprimer sa démonstration pour résoudre le probléme...
Merci

par **annick** » 13 Oct 2012, 18:31

Si tu lis bien, je t'ai donné les pistes pour effectuer ta démonstration :
quelles sont les coordonnées de S en fonction de b ?

par **superphyl** » 13 Oct 2012, 18:36

Bonsoir... je dois aller prendre mon repas et on reprend demain.
Merci et @ demain ??? ^^

Pas d'idée pour la résolution ??

Pas d'idée pour la résolution ??

Qui est en ligne