DM pas facile
14 messages
- Page 1 sur 1
DM pas facile
Bonjour cher matheux....
voila, je suis en 1ere S dans un lycée qui veut sa belle réputation de 100% au BAC, je ne le citerais point...
J'ai un prof cet année très très bon, qui donne des bons devoirs a te casser le cerveau...enfin à chercher....
voila je présente mon probleme, je souhaiterai savoir si mon raisonnement est bon? c'est devoir maison à rendre...
Résoudre dans R suivant les valeurs du paramètre réel m,
m(m+1)x²-(2m²+1)x+m(m+1) =0
a=m(m+1)
b=-(2m²+1)
c=m(m+1)
donc j'ai déjà la un problème se pose:
je pose donc m(m+1) différent de 0 soit m different de 0 ?
puis j'ai calculer son delta majuscule :
j'ai trouvé -2m²(2m²+4m+3) + 1
et la ca bloque....
s'il vous plait, j'ai besoin d'aide...
Merci beaucoup d'avance
voila, je suis en 1ere S dans un lycée qui veut sa belle réputation de 100% au BAC, je ne le citerais point...
J'ai un prof cet année très très bon, qui donne des bons devoirs a te casser le cerveau...enfin à chercher....
voila je présente mon probleme, je souhaiterai savoir si mon raisonnement est bon? c'est devoir maison à rendre...
Résoudre dans R suivant les valeurs du paramètre réel m,
m(m+1)x²-(2m²+1)x+m(m+1) =0
a=m(m+1)
b=-(2m²+1)
c=m(m+1)
donc j'ai déjà la un problème se pose:
je pose donc m(m+1) différent de 0 soit m different de 0 ?
puis j'ai calculer son delta majuscule :
j'ai trouvé -2m²(2m²+4m+3) + 1
et la ca bloque....
s'il vous plait, j'ai besoin d'aide...
Merci beaucoup d'avance
Salut,
tu as bien commencé ton raisonnement:
1) si m(m+1)=0 alors l'équation devient (2m²+1)x =0
Or m(m+1)=0 implique m=0 ou m=-1, on a donc deux cas qui se présentent:
Si m=0 alors l'équation devient x=0
Si m=-1 alors l'équation devient 3x=0
Dans les deux cas, la solution est 0.
2) si m(m+1) est différent de 0 alors on a une équation du second degré.
On a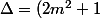^2-4\times m(m+1)\times m(m+1))
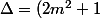^2-4m^2(m+1)^2)
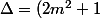^2-(2m(m+1))^2)
On reconnaît une expression de la forme A²-B², ce qui nous permet de factoriser
Je te laisse terminer (la discussion tourne ensuite autour de m=1/2)
Salut.
:happy3:
tu as bien commencé ton raisonnement:
1) si m(m+1)=0 alors l'équation devient (2m²+1)x =0
Or m(m+1)=0 implique m=0 ou m=-1, on a donc deux cas qui se présentent:
Si m=0 alors l'équation devient x=0
Si m=-1 alors l'équation devient 3x=0
Dans les deux cas, la solution est 0.
2) si m(m+1) est différent de 0 alors on a une équation du second degré.
On a
On reconnaît une expression de la forme A²-B², ce qui nous permet de factoriser
Je te laisse terminer (la discussion tourne ensuite autour de m=1/2)
Salut.
:happy3:
petit +
Bonjour,
Je souhaiterai demander quelques tuyaux pour la rédaction ( à cause du prof très matheux :marteau: )
Donc voilà mon étude:
m(m+1)x²-(2²m+1)x+m(m+1)=0 [E]
****Si m=0 ou m=-1 alors [E] devient,****
0(0+1)x²-(2*0²+1)x+0(0+1)=0
0x²-x+0=0 soit x=0
ou
(-1)(-1+1)x²-(2*(-1)²+1)x+(-1)(-1+1)=0
0x²-x+0=0 soit x=0
****Si m est différent de 0 ou m est different de -1 alors [E] devient, *****
m(m+1)x²-(2m²+1)x+m(m+1)=0
avec a=m(m+1)
b=-(2m²+1)
c=m(m+1)
Calcul de delta majuscule appelé D :
D = b²-4ac
D = (-(2m²+1))²-4(m(m+1))²
D = (2m²+1)² - (2m²+2m)²
D = (2m²+1-2m²-2m)(2m²+1+2m²+2m)
D = (-2m+1)(4m²+2m+1)
A partir de là, je ne sais pas présenter la rédaction pour trouver m et ainsi dire si D est positif,négatif ou nul.
J'appel a l'aide. Merci Beaucoup d'avance.
VIVE LES MATHEMATIQUES
David :zen:
Je souhaiterai demander quelques tuyaux pour la rédaction ( à cause du prof très matheux :marteau: )
Donc voilà mon étude:
m(m+1)x²-(2²m+1)x+m(m+1)=0 [E]
****Si m=0 ou m=-1 alors [E] devient,****
0(0+1)x²-(2*0²+1)x+0(0+1)=0
0x²-x+0=0 soit x=0
ou
(-1)(-1+1)x²-(2*(-1)²+1)x+(-1)(-1+1)=0
0x²-x+0=0 soit x=0
****Si m est différent de 0 ou m est different de -1 alors [E] devient, *****
m(m+1)x²-(2m²+1)x+m(m+1)=0
avec a=m(m+1)
b=-(2m²+1)
c=m(m+1)
Calcul de delta majuscule appelé D :
D = b²-4ac
D = (-(2m²+1))²-4(m(m+1))²
D = (2m²+1)² - (2m²+2m)²
D = (2m²+1-2m²-2m)(2m²+1+2m²+2m)
D = (-2m+1)(4m²+2m+1)
A partir de là, je ne sais pas présenter la rédaction pour trouver m et ainsi dire si D est positif,négatif ou nul.
J'appel a l'aide. Merci Beaucoup d'avance.
VIVE LES MATHEMATIQUES
David :zen:
On ne veut pas chercher m. On veut déterminer, suivant les valeurs de m, le signe de Delta.
Delta est ici sous forme d'un produit de facteurs. Pour étudier son signe, il faut faire un tableau de signes.
Ok pour le signe de -2m+1
Il y a pb pour le signe de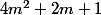
C'est un trinôme du second degré de la variable m. On calcule son discriminant petitdelta, qui vaut -12. Ce discriminant étant négatif, le polynôme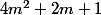 ne s'annule jamais, et est du signe du coefficient de
ne s'annule jamais, et est du signe du coefficient de 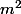 , donc positif.
, donc positif.
On a finalement : si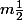 Delta est ...
Delta est ...
Delta est ici sous forme d'un produit de facteurs. Pour étudier son signe, il faut faire un tableau de signes.
Ok pour le signe de -2m+1
Il y a pb pour le signe de
C'est un trinôme du second degré de la variable m. On calcule son discriminant petitdelta, qui vaut -12. Ce discriminant étant négatif, le polynôme
On a finalement : si
autre problème
Bonjour,
Je souhaite remercier ceux ki on répondu ou lu mon topic... :we:
J'ai un exercice autre ki me pose probleme:
Donc voilà l'énoncé :
On considère l'équation [E] : mx²-2(m+2)x+3m+4=0
1) Etudier l'existence des solutions x' et x''
Ici je trouve qu'il y a des solutions pour tout m [-V2 ; V2 ]
V= racine carrée de
2) Déterminer m tel que 1/x' + 1/x'' = 12
J'ai trouvé un truc bizarre :doh: environ 0.04 et 1.2
3) Déterminer m tel que l'une des solutions est triple de l'autre
gros probleme
4) Etablir une relation indépendant de m liant x' et x''. Pour cela, on pourra introduire S et P, somme et produit des racines et obtenir une relation entre S et P indépendante de m.
jorai sil vous plait grands matheux :id: besoin de votre aide
merci
David
Je souhaite remercier ceux ki on répondu ou lu mon topic... :we:
J'ai un exercice autre ki me pose probleme:
Donc voilà l'énoncé :
On considère l'équation [E] : mx²-2(m+2)x+3m+4=0
1) Etudier l'existence des solutions x' et x''
Ici je trouve qu'il y a des solutions pour tout m [-V2 ; V2 ]
V= racine carrée de
2) Déterminer m tel que 1/x' + 1/x'' = 12
J'ai trouvé un truc bizarre :doh: environ 0.04 et 1.2
3) Déterminer m tel que l'une des solutions est triple de l'autre
gros probleme
4) Etablir une relation indépendant de m liant x' et x''. Pour cela, on pourra introduire S et P, somme et produit des racines et obtenir une relation entre S et P indépendante de m.
jorai sil vous plait grands matheux :id: besoin de votre aide
merci
David
S'il vous plait
S'il vous plait, j'aimerai vraiment que vous m'aidiez pour la question c et d de mon exercice.
David
Merci d'avance :we:
David
Merci d'avance :we:
désolé
désolé je me suis trompé....
Aidez moi à résoudre la question 3 et 4 :hum: c dur :doh:
merci d'avance
jsouhaiterai juste la méthode
Aidez moi à résoudre la question 3 et 4 :hum: c dur :doh:
merci d'avance
jsouhaiterai juste la méthode
Bonjour,
1) attention au cas particulier m = 0
2) je n'obtient pas les mêmes valeurs
pour la 2) la 3) et la 4) il faut investir à fond les propriétés
x' + x" = - b / a et x"x' = c/a
pour la 2)
cela donne une équation simple à résoudre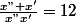
pour la 3)
il suffit de poser x" = 3x' pour obtenir
4x' = -b/a et 3x'² = c/a
en remplaçant x' par -b/(4a) dans la deuxième équation tu tombes sur une condition sur m qu'il te suffit d'exploiter. il te faut ensuite vérifier si tout marche bien
pour la 4)
cela donne
S = 2 +4/m et P = 3 + 4/m
Il te suffit d'exprimer dans la première égalité, 4/m en fonction de S et de remplacer dans la seconde et tu auras une relation entre S et P (donc entre x' et x" ) indépendante de m
Bon courage
1) attention au cas particulier m = 0
2) je n'obtient pas les mêmes valeurs
pour la 2) la 3) et la 4) il faut investir à fond les propriétés
x' + x" = - b / a et x"x' = c/a
pour la 2)
cela donne une équation simple à résoudre
pour la 3)
il suffit de poser x" = 3x' pour obtenir
4x' = -b/a et 3x'² = c/a
en remplaçant x' par -b/(4a) dans la deuxième équation tu tombes sur une condition sur m qu'il te suffit d'exploiter. il te faut ensuite vérifier si tout marche bien
pour la 4)
cela donne
S = 2 +4/m et P = 3 + 4/m
Il te suffit d'exprimer dans la première égalité, 4/m en fonction de S et de remplacer dans la seconde et tu auras une relation entre S et P (donc entre x' et x" ) indépendante de m
Bon courage
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
