Salut à tous besoin d'aide je n'arrive pas à démarrer
E(x) dsigne la partie entière du réel x, déterminer E(x^x) pour x€ ]0;1[
Partie entière
7 messages
- Page 1 sur 1
Re: Partie entière
Bonjour
Tu étudies les variations de=x^x) sur ]0,1[. C'est vraiment pas compliqué.
sur ]0,1[. C'est vraiment pas compliqué.
Pour trouver E[f(x)]=0.
Tu étudies les variations de
Pour trouver E[f(x)]=0.
Modifié en dernier par aviateur le 09 Juil 2019, 11:16, modifié 1 fois.
Re: Partie entière
Salut,
Etudie la fonction f(x) = x^x
Que vaut f'(x) ? Quelles sont les variations de f sur ]0 ; 1[ ?
Que vaut la limite de f sur les bords de ]0 ; 1[ ?
Etudie la fonction f(x) = x^x
Que vaut f'(x) ? Quelles sont les variations de f sur ]0 ; 1[ ?
Que vaut la limite de f sur les bords de ]0 ; 1[ ?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Re: Partie entière
Salut !
Montre que pour tout , on a
, on a  \in {]} \ln(x),0 {[}) .
.
Déduis-en alors que puisque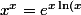}) , on a
, on a =0) .
.
Montre que pour tout
Déduis-en alors que puisque
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Partie entière
Bonjour,
x^x=e^lnx*x
sur [0;1] ln x dans ]-infini;0[ donc xlnx dans ]-1;0[ donc e^xln(x) dans [0;1] donc E[x^x] =0 dans [0;1]
x^x=e^lnx*x
sur [0;1] ln x dans ]-infini;0[ donc xlnx dans ]-1;0[ donc e^xln(x) dans [0;1] donc E[x^x] =0 dans [0;1]
Re: Partie entière
Bonjour ;
Une autre façon de faire .
Soit la fonction définie sur
la fonction définie sur 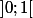 par :
par :  = x^x = e^{x\ ln(x)}) .
.
 est dérivable sur
est dérivable sur 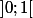 , donc on a :
, donc on a :  = (x\ ln(x))'e^{x\ ln(x)} = (1 + ln(x))e^{x\ ln(x)}) .
.
 est du signe de
est du signe de ) ;
;
donc est strictement négative sur
est strictement négative sur 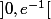 ; strictement positive sur
; strictement positive sur 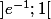 et s'annule pour x = e^{-1} ;
et s'annule pour x = e^{-1} ;
donc est strictement décroissante sur
est strictement décroissante sur 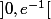 ; strictement croissante sur
; strictement croissante sur 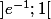 et admet un minimum pour
et admet un minimum pour 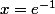 .
.
On a : = e^{-\frac{1}{e}}) ;
; =\underset{x\rightarrow 1^-}{lim}f(x)=1) .
.
Conclusion :
\in ]e^{-\frac{1}{e}} ; 1[) ;
;
donc :) = 0) .
.
Une autre façon de faire .
Soit
donc
donc
On a :
Conclusion :
donc :
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
