Parité fonction exponentielle

[LuluCooooper]

Bonsoir !!

Je dois vérifier que la fonction est impaire.

puis comparer g'(x) avec 1-g²(x).

J'ai essayé de faire g(-x) et -g(x), je ne trouve pas pareil !



et

-

Pour la dérivée je trouve 0 lol...

Merci d'avance pour votre aide !

[Ericovitchi]

Pourtant ton g(-x) est bien - g(x) , regardes mieux

(et quand on fait - à une fraction, on ne fait pas - en haut et en bas, on fait - en haut seulement sinon ça ne change rien)

Montres tes calculs de g', on te dira où ça va pas.

[LuluCooooper]

Pour -g(x) j'ai changé tous les signes cest pas bon ?

Quand on fait l'opposé d'un quotient on change les signe uniquement du numérateur ?

Pour g' :



Cest bon deja la ?

[Ericovitchi]

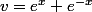
non le v' de ne va pas c'est v=

débrouilles toi pour simplifier il faut que tu trouves
= à cause de la suite évidemment

[LuluCooooper]

OK

juste avant : oui ?

[LuluCooooper]

Je trouve :


et quand je développe 1-g²(x) je trouve pareil.

[LuluCooooper]

Bonjour !

J'ai un calcul de limite a faire :

en plus et moins l'infini de

et après que dire de la droite d:y=-x+1.

J'ai fait la limite en plus infini en mettant e^x en facteur, je trouve +infini.

Mais pour moins infini je sais pas comment faire ?

Puisque ca fait 0(1-0+0)

Merci d'avance pour votre aide !

[LuluCooooper]

Ah zut jai mal fait mon sujet;... DESOLEE

[LuluCooooper]

Je trouve :


et quand je développe 1-g²(x) je trouve pareil.

Peut on me dire sil vous plait si c'est juste la dérivée... merci

[Laurent Porre]

Peut on me dire sil vous plait si c'est juste la dérivée... merci

c'est juste bravo :we:

[LuluCooooper]

c'est juste bravo :we:

ENFIN ! Merci beaucoup !

A bientot