Orthogonalité, 1ère S.
22 messages
- Page 1 sur 2 - 1, 2
Orthogonalité, 1ère S.
Bonjour ! =D
J'ai un exercice à faire sur l'orthogonalité, et je suis... Bloqué, pour changer ^^'
Voilà l'énoncé :
Dans le repère orthonormal (O ; i, j), on donne les points A (-2 ; 2) et B (1 ; 1).
1) Déterminer les points M de l'axe (O ; i), tels que les droites (AM) et (BM) soient orthogonales.
2) Déterminer les points N de l'axe (O ; j), tels que le triangle ABN soit rectangle en N.
3) On désigne par M1 et N1 les points autres que O trouvés aux questions précédentes. Démontrer que le quadrilatère AM1BN1 est un carré.
Pour la première question, est-ce que quelqu'un peut m'orienter ? Par quoi dois-je commencer ?
J'ai un exercice à faire sur l'orthogonalité, et je suis... Bloqué, pour changer ^^'
Voilà l'énoncé :
Dans le repère orthonormal (O ; i, j), on donne les points A (-2 ; 2) et B (1 ; 1).
1) Déterminer les points M de l'axe (O ; i), tels que les droites (AM) et (BM) soient orthogonales.
2) Déterminer les points N de l'axe (O ; j), tels que le triangle ABN soit rectangle en N.
3) On désigne par M1 et N1 les points autres que O trouvés aux questions précédentes. Démontrer que le quadrilatère AM1BN1 est un carré.
Pour la première question, est-ce que quelqu'un peut m'orienter ? Par quoi dois-je commencer ?
Bonjour.
Il y a deux points qui sont l'intersection du cercle de diametre AB avec l'axe des abscisses.
Tu calcules la longueur de AB
Tu calcules les coordonnées du milieu de AB
Tu calcules les deux points M distants de ce milieu de la longueur AB/2
1) Déterminer les points M de l'axe (O ; i), tels que les droites (AM) et (BM) soient orthogonales.
Il y a deux points qui sont l'intersection du cercle de diametre AB avec l'axe des abscisses.
Tu calcules la longueur de AB
Tu calcules les coordonnées du milieu de AB
Tu calcules les deux points M distants de ce milieu de la longueur AB/2
Merci pour vos réponses, et désolé de ne pas avoir pu répondre plus tôt. =D
Phryte : J'ai AB ( ), les coordonnées du milieu de AB :
), les coordonnées du milieu de AB :
I ( - ;
; 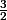 )
)
Je ne comprend par contre pas la marche à suivre dans le troisième point que tu as énoncé, à savoir "calculer les deux points M distants de ce milieu de la longueur AB/2"... Peux-tu éclairer ma lanterne ?
Phryte : J'ai AB (
I ( -
Je ne comprend par contre pas la marche à suivre dans le troisième point que tu as énoncé, à savoir "calculer les deux points M distants de ce milieu de la longueur AB/2"... Peux-tu éclairer ma lanterne ?
Je ne comprend par contre pas la marche à suivre dans le troisième point que tu as énoncé, à savoir "calculer les deux points M distants de ce milieu de la longueur AB/2"... Peux-tu éclairer ma lanterne ?
Donc :
3/2 + racine(10)/2
3/2 - racine(10)/2
Pas sûr (il faut faire Pythagore) ! (XENSECP a raison sa solution est plus courte et surtout plus élégante)
Bonjour.
L'équation du cercle est : (x+0.5)^2+(y-1.5)^2=2.5
Pour x = 0 :
y^2-*3y=0
y(y-3)=0
et les points N sont :
N1(0;0)
N2(0;3)
[img][IMG]http://img164.imageshack.us/img164/300/cerclefk7.jpg[/img] [/IMG]
[/IMG]
L'équation du cercle est : (x+0.5)^2+(y-1.5)^2=2.5
Pour x = 0 :
y^2-*3y=0
y(y-3)=0
et les points N sont :
N1(0;0)
N2(0;3)
[img][IMG]http://img164.imageshack.us/img164/300/cerclefk7.jpg[/img]
 [/IMG]
[/IMG]
22 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
