Ordre

[moullmat]

salut, comment montrer que a/b+b/c+c/a est supérieur ou égal à 3 tel que a b et c sont des réels strictement positifs.je le cherche depuis des mois.

[Sylviel]

Bonjour je pense que je commencerais que je peux me ramener à chercher le minimum sur x et y positif de
1/x + x/y + y.

Puis à y fixé cherche le minimum en x, et minimise ensuite par rapport à y.

[Ericovitchi]

Si on sait que la moyenne géométrique est toujours plus petite que la moyenne arithmétique alors c'est évident.
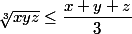
on fait x = a/b ; y = b/c et z = c/a dans cette inégalité.

la démonstration moyenne géométrique <= moyenne arithmétique est classique.