Ordre dans R
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
nicolas360
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Jan 2012, 01:41
-
 par nicolas360 » 24 Jan 2012, 16:54
par nicolas360 » 24 Jan 2012, 16:54
Bonjour,
Il y a un exemple dans mon cours par correpondance de Premiere S que je comprends pas du tout. Je tiens a rappeller que j' avais arreter les cours de math depuis 2 ans maintenant.
Montrer que pour tout a de R, a^2 + 1 >= 2a
Solution :
Etudions le signe de la difference.
On a : (a^2 + 1 ) - ( 2a ) = a^2 - 2a + 1 = ( a - 1 )^2 >= 0
On en deduit l' inegalite : a^2 + 1 >= 2a
En fait, je ne comprends pas comment il sont arrive a ce que j'ai mis en gras.
Je vous remercie.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 24 Jan 2012, 17:01
par Carpate » 24 Jan 2012, 17:01
nicolas360 a écrit:Bonjour,
Il y a un exemple dans mon cours par correpondance de Premiere S que je comprends pas du tout. Je tiens a rappeller que j' avais arreter les cours de math depuis 2 ans maintenant.
En fait, je ne comprends pas comment il sont arrive a ce que j'ai mis en gras.
Je vous remercie.
Sur R,
^2 \geq 0)
En développant et en isolant

...
-
nicolas360
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Jan 2012, 01:41
-
 par nicolas360 » 24 Jan 2012, 17:03
par nicolas360 » 24 Jan 2012, 17:03
Desole, je ne comprends pas... :mur:
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 24 Jan 2012, 17:04
par Carpate » 24 Jan 2012, 17:04
nicolas360 a écrit:Desole, je ne comprends pas... :mur:
Qu'est-ce que tu ne comprends pas exactement ?
-
nicolas360
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Jan 2012, 01:41
-
 par nicolas360 » 24 Jan 2012, 17:09
par nicolas360 » 24 Jan 2012, 17:09
Je ne comprends pas, comment on arrive de
a^2 - 2a + 1
a
( a - 1 )^2 >= 0
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 24 Jan 2012, 17:15
par Carpate » 24 Jan 2012, 17:15
nicolas360 a écrit:Je ne comprends pas, comment on arrive de a
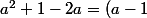^2)
Le carré d'une expression réelle ne peut pas être négatif.
Je ne te ferais pas l'injure de croire que tu ne sais pas passer de

à

-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 24 Jan 2012, 17:15
par Dinozzo13 » 24 Jan 2012, 17:15
SAalut !
Il s'agit de l'identité remarquable :
^2=a^2+2ab+b^2)
.
Or quel que soit

et

dans

:
^2\ge 0)
donc ...
-
nicolas360
- Membre Naturel
- Messages: 16
- Enregistré le: 24 Jan 2012, 01:41
-
 par nicolas360 » 24 Jan 2012, 17:21
par nicolas360 » 24 Jan 2012, 17:21
Ah, d'accord, j'ai compris !
Merci beaucoup :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 81 invités
