Comment résoudre ce problème ?
Il y a plusieurs paires de nombres (positifs et/ou négatifs) dont la somme vaut lunité.
Parmi ceux-ci, trouvez les deux nombres dont la somme du double du carré du premier
nombre et du cube du second nombre donnerait une valeur maximale relative.
Optimisation
3 messages
- Page 1 sur 1
Re: optimisation
par MJoe » 02 Aoû 2017, 06:28
Bonjour à tous,
Il faut "mettre en équation".
Si on note x et y ces deux nombres alors x + y = 1
On obtient :
=2x^{2}+y^{3}\;soit\;g(x)=2x^{2}+(1-x)^{3}\;car\;y=(1-x))
Il faut développer l'expression de)
puis étudier les variations de g afin de définir le maximum demandé.
MJoe.
Il faut "mettre en équation".
Si on note x et y ces deux nombres alors x + y = 1
On obtient :
Il faut développer l'expression de
MJoe.
Re: optimisation
par MJoe » 02 Aoû 2017, 17:30
Bonjour à tous,
Un petit graphique avec Geogebra :
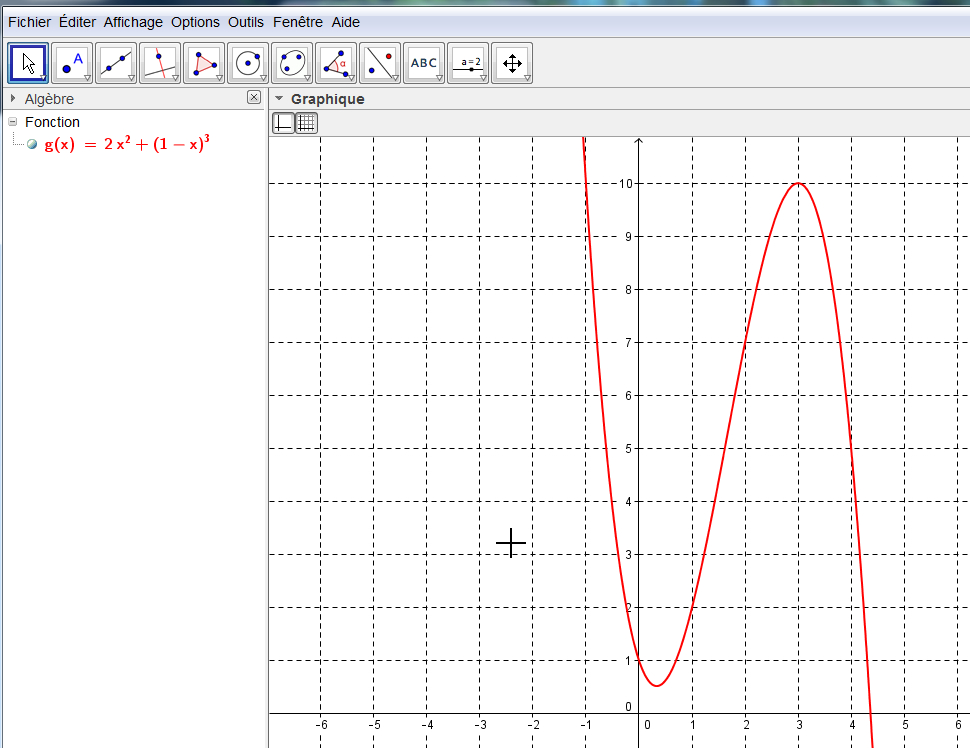
On obtient donc un maximum relatif égal à 10 pour x = 3 et y = -2
MJoe.
Un petit graphique avec Geogebra :
On obtient donc un maximum relatif égal à 10 pour x = 3 et y = -2
MJoe.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :