Bonjour à vous, je suis exposé à un problème surement basique mais pourtant délicat à résoudre pour moi.
J'ais à ma disposition un trapèze dont la longueur et la hauteur me sont connues, plus la longueur d'arête. Je dois déterminer quel serait la surface rectangulaire ( ou carré ) maximale que je peux y mettre à l'intérieur.
Données: Lo, Larête et H pour le trapèze
Inconnues: L, l pour le rectangle recherché.
Auriez vous une idée?
Optimisation de surface
8 messages
- Page 1 sur 1
Longueur d'arete, pour moi c'est la longueur du sommet du trapèze.
Je pensais aux dérivés, mais je ne vois pas comment faire.
J'avais réfléchis aussi à ne prendre que le rectangle dont la longueur serait celle de l'arête et la largeur serait la hauteur du trapèze ( on sait qu'un trapèze c'est plus ou moins un rectangle auquel on a acollé deux triangles ) mais parfois ce rectangle la n'est pas le plus grand que l'ont peut avoir dans un trapèze ( cas extreme ou la longueur d'arete est nulle, auquel ca on se retrouve avec un triangle )
Je parle d'arête car dans mon cas ce trapèze représente un toit, et j'assimile la longueur à la grande base, la longueur d'arête représente la petite base si l'on se réfère aux termes général.
Je pensais aux dérivés, mais je ne vois pas comment faire.
J'avais réfléchis aussi à ne prendre que le rectangle dont la longueur serait celle de l'arête et la largeur serait la hauteur du trapèze ( on sait qu'un trapèze c'est plus ou moins un rectangle auquel on a acollé deux triangles ) mais parfois ce rectangle la n'est pas le plus grand que l'ont peut avoir dans un trapèze ( cas extreme ou la longueur d'arete est nulle, auquel ca on se retrouve avec un triangle )
Je parle d'arête car dans mon cas ce trapèze représente un toit, et j'assimile la longueur à la grande base, la longueur d'arête représente la petite base si l'on se réfère aux termes général.
Tu peux toujours essayer d'optimiser la surface du rectangle :
 en calculant la surface de ce rectangle en fonction des cotés et/ou angles du trapèze ainsi que de x et dériver pour rechercher les maximums mais en gardant des valeurs littérales partout, ça va être un peu fastidieux à calculer dans un cas quelconque. Tu n'as pas de valeurs précises pour le trapèze ?
en calculant la surface de ce rectangle en fonction des cotés et/ou angles du trapèze ainsi que de x et dériver pour rechercher les maximums mais en gardant des valeurs littérales partout, ça va être un peu fastidieux à calculer dans un cas quelconque. Tu n'as pas de valeurs précises pour le trapèze ?
 en calculant la surface de ce rectangle en fonction des cotés et/ou angles du trapèze ainsi que de x et dériver pour rechercher les maximums mais en gardant des valeurs littérales partout, ça va être un peu fastidieux à calculer dans un cas quelconque. Tu n'as pas de valeurs précises pour le trapèze ?
en calculant la surface de ce rectangle en fonction des cotés et/ou angles du trapèze ainsi que de x et dériver pour rechercher les maximums mais en gardant des valeurs littérales partout, ça va être un peu fastidieux à calculer dans un cas quelconque. Tu n'as pas de valeurs précises pour le trapèze ?Je me suis rendu compte que j'ais pas posté sur le bon forum, car je cherchais une solution pouvant être exploité sous visual basic par la suite.
Dans mon cas, j'ais un trapèze isocèle.
J'ai trouvé une solution, bien que très lourde sur le papier, mais gérable sous un langage de programmation.
J'ai donc calculé la surface rectangulaire de base ( en virant les deux triangles qui compose le trapèze ) puis j'ais exprimé longueur et largeur en fonction d'une même variable ( i )
ce qui donne pour la formule de l'aire du rectangle:
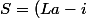 * (Lare + i * x / (La))) hauteur longueur
hauteur longueur
Avec -La la hauteur du trapèze
-Lare la longueur d'arête ( ou petite base du trapèze )
-x étant la différence entre la Longeur ( grande base ) et la longueur d'arete ( petite base )
je fais ensuite varier i entre 0 et La, ce qui donne une variation entre 0 et la hauteur pour le premier terme, et 0 et la longueur de la grande base pour le second terme.
Je détermine ensuite la surface maximale en cherchant le max des surface préalablement calculé.
Je cherchais comment faire via les dérivés, avec ma fonction, ce qui donnerais:
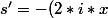/La + x-Lare) que je dois annuler afin d'avoir un extremum:
que je dois annuler afin d'avoir un extremum:
d'ou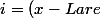/(2*x))
Ce qui me donne bien le même résultat que via ma routine sous VB.
Je prend ensuite, pour vérifier, si mon i trouvé est bien un max et non un min, donc je regarde le signe de la dérivé seconde, qui, étant négatif, me confirme que c'est le maximum.
Mon raisonnement sur les dérivés tient il la route ?
Dans mon cas, j'ais un trapèze isocèle.
J'ai trouvé une solution, bien que très lourde sur le papier, mais gérable sous un langage de programmation.
J'ai donc calculé la surface rectangulaire de base ( en virant les deux triangles qui compose le trapèze ) puis j'ais exprimé longueur et largeur en fonction d'une même variable ( i )
ce qui donne pour la formule de l'aire du rectangle:
Avec -La la hauteur du trapèze
-Lare la longueur d'arête ( ou petite base du trapèze )
-x étant la différence entre la Longeur ( grande base ) et la longueur d'arete ( petite base )
je fais ensuite varier i entre 0 et La, ce qui donne une variation entre 0 et la hauteur pour le premier terme, et 0 et la longueur de la grande base pour le second terme.
Je détermine ensuite la surface maximale en cherchant le max des surface préalablement calculé.
Je cherchais comment faire via les dérivés, avec ma fonction, ce qui donnerais:
d'ou
Ce qui me donne bien le même résultat que via ma routine sous VB.
Je prend ensuite, pour vérifier, si mon i trouvé est bien un max et non un min, donc je regarde le signe de la dérivé seconde, qui, étant négatif, me confirme que c'est le maximum.
Mon raisonnement sur les dérivés tient il la route ?
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
