Opération sur n!
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 29 Sep 2012, 16:59
par Anonyme » 29 Sep 2012, 16:59
sleepy a écrit:C'est dur quand même pour une T°S. ^^
En espérant avoir mon cinquième 20 en maths de l'année ^^
Non a priori ce n'est pas dur
De plus les exos de type BAC indique toujours en général quand il faut faire une récurrence
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 16:59
par Kikoo <3 Bieber » 29 Sep 2012, 16:59
sleepy a écrit:C'est dur quand même pour une T°S. ^^
En espérant avoir mon cinquième 20 en maths de l'année ^^
Haha 20 en TS c'est facile !!! C'est nul, tout est trivial, bâteau, tout passe crème, lol.
C'est bien, bon courage pour la suite

-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:03
par sleepy » 29 Sep 2012, 17:03
Kikoo <3 Bieber a écrit:Haha 20 en TS
c'est facile !!! C'est nul, tout est trivial, bâteau, tout passe crème, lol.
C'est bien, bon courage pour la suite

Va dire ça aux 28 autres qui ont moins ^^
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 17:06
par Kikoo <3 Bieber » 29 Sep 2012, 17:06
Je plaisante ! Mais en prenant du recul, la TS c'était vraiment une partie de plaisir par rapport à ce que j'ai maintenant.
Me trompé-je ou me semble-t-il que tu manques d'humilité ? ;)
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:07
par sleepy » 29 Sep 2012, 17:07
Tu es dans quelle prépa MPSI ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 17:11
par Kikoo <3 Bieber » 29 Sep 2012, 17:11
sleepy a écrit:Tu es dans quelle prépa MPSI ?
PCSI. Tu peux le voir dans mon profil.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:16
par sleepy » 29 Sep 2012, 17:16
Ca fait 4h que je bosse j'ai plus de cerveau, avant dernière question :
on a v²n+1 - u²n+1 = [(Un-Vn)/2]²
En déduire que Un
SVP >.<
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 17:19
par Kikoo <3 Bieber » 29 Sep 2012, 17:19
sleepy a écrit:Ca fait 4h que je bosse j'ai plus de cerveau, avant dernière question :
on a v²n+1 - u²n+1 = [(Un-Vn)/2]²
En déduire que Un.<
C'est mal écrit, comment indices-tu tes suites ? Des parenthèses qui manquent ?
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:34
par sleepy » 29 Sep 2012, 17:34
on a
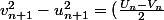^2)
En déduire que

On a aussi

et
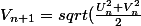)
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:45
par sleepy » 29 Sep 2012, 17:45
Personne sait?
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 17:53
par sleepy » 29 Sep 2012, 17:53
Est ce que c'est correct de dire :

donc

??
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 17:57
par Kikoo <3 Bieber » 29 Sep 2012, 17:57
sleepy a écrit:Est ce que c'est correct de dire :

donc

??
Pas rigoureux, et c'est parfois faux, pour cela vaut mieux faire un raisonnement par récurrence.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 17:58
par Kikoo <3 Bieber » 29 Sep 2012, 17:58
Aaaah tu as réécrit ton expression comme il faut ! :) Ca fait plaisir
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 18:01
par sleepy » 29 Sep 2012, 18:01
La question c'est "EN DÉDUIRE que, pour tout entier naturel n, on a

"
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 18:02
par Kikoo <3 Bieber » 29 Sep 2012, 18:02
sleepy a écrit:on a
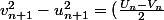^2)
En déduire que

On a aussi

et
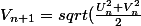)
En fait pour cela, il faut donner :
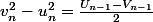^2)
qui est valide par changement d'indice.
Or montrer que

revient à montrer que

qui équivaut à :

Ce qui est toujours vrai.
FIN.
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 18:03
par Kikoo <3 Bieber » 29 Sep 2012, 18:03
sleepy a écrit:La question c'est "EN DÉDUIRE que, pour tout entier naturel n, on a

"
Non mais tout à l'heure t'avais marqué
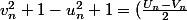^2)
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 18:09
par sleepy » 29 Sep 2012, 18:09
Merci :)
___

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 29 Sep 2012, 18:19
par fatal_error » 29 Sep 2012, 18:19
montrer que

revient à montrer que

qui équivaut à :

attention.
on a v_n^2-u_n^2=(v_n-u_n)(v_n+u_n)>0 (v_n-u_n) et (v_n+u_n) de même signe.
On cherche v_n-u_n>0 idem il faut montrer que nécessairement on a u_n+v_n>0
sinon on peut pas conclure
la vie est une fête

-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 29 Sep 2012, 18:23
par Kikoo <3 Bieber » 29 Sep 2012, 18:23
C'est vrai, tu as tout à fait raison fatal_error.
Je suppose qu'il doit quand même y avoir une donnée qui stipule que (u) et (v) sont toutes les deux positives.
-
sleepy
- Membre Naturel
- Messages: 22
- Enregistré le: 29 Sep 2012, 14:13
-
 par sleepy » 29 Sep 2012, 18:25
par sleepy » 29 Sep 2012, 18:25
Ben non car on sait que v²_n-u²_n > 0
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités